Question

已知数列{a_n}的前n项和为S_n,a₁=1,S_n+1=2S_n+3n+1(n∈N^*).

(1)证明数列{a_n+3}是等比数列;

(2)对k∈N^*,设f(n)=求使不等式f(m)＞f(2m²)成立的自然数m的最小值.

(文)对a、b∈R,已知等差数列{a_n}的首项为a,公差为b,前n项和;等比数列{b_n}的首项为b,公比为a.

(1)求数列{a_n}、{b_n}的通项公式a_n、b_n;

(2)对k∈N^*,设f(n)=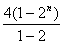若存在正整数m使f(m+11)=2f(m)成立,求数列{f(n)}的前10m项的和.

Answer 1

(理)(1)证明:∵a₁=1,S_n+1=2S_n+3n+1,

∴S₂=2S₁+4=a₁+a₂.

∴a₂=5.

又当n≥2时,S_n=2S_n-1+3(n-1)+1,

∴S_n+1-S_n=2(S_n-S_n-1)+3,即得a_n+1=2a_n+3.

可变形为a_n+1+3=2(a_n+3).

∴=2(n≥2).

而,

∴数列{a_n+3}是公比为2,首项为a₁+3=4的等比数列.

(2)解:由(1),知a_n+3=4·2^n-1.

∴a_n=2ⁿ⁺¹-3,S_n=-3n=2ⁿ⁺²-3n-4.

∴f(n)=(k∈N^*).

①当m为偶数时,

∵f(m)=m+1,f(2m²)=2m²+1,

∴不存在自然数m,使f(m)＞f(2m²)恒成立.

②当m为奇数时,f(m)=2^m+1-1,

f(2m²)=2m²+1,而f(m)＞f(2m²),

当m=1时,f(m)=2¹⁺¹-1=3=f(2m²)=3;

当m=3时,f(m)=2³⁺¹-1=15＜f(2m²)=19;

当m=5时,f(m)=2⁵⁺¹-1=63＞f(2m²)=51;

又当m≥5时,f(m)=2^m+1-1=2·2^m-1

=2(1+)-1

≥2m²+2m+3＞2m²+1=f(2m²).

即当m≥5且为奇数时,f(m)＞f(2m²)成立,

此时m的最小值为5.

(也可用数学归纳法证明上述结果)

综上可知,使f(m)＞f(2m²)成立的自然数m的最小值为5.

(文)解:(1)∵S_n=n²-n,

∴a=a₁=S₁=2,a₂=S₂-S₁=7,b=a₂-a₁=5.

∴a_n=5n-3(n∈N^*),

b_n=5·2^n-1(n∈N^*).

(2)由(1)知,

f(n)=k∈N^*).

①若m是正偶数,则m+11是正奇数.

故f(m+11)=m+10,f(m)=2m-1.

代入f(m+11)=2f(m)中,得m+10=2(2m-1),解得m=4.7分

②若m是正奇数,则m+11是正偶数,则f(m+11)=2(m+11)-1=2m-21,f(m)=m-1.

代入f(m+11)=2f(m)中,得2m-21=2(m-1),解得19=0,显然不成立,此时m不存在.9分

故所求m=4.

设{f(n)}的前n项和为S_n,则S₁₀m=S₄₀=(0+2+4+…+38)+(3+7+11+…+79)

=

=1 200.