题目内容
已知命题P:4-2x≥0;命题q;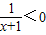 ,若p∧(¬q)为真命题,求x的取值范围.
,若p∧(¬q)为真命题,求x的取值范围.
【答案】分析:解一次不等式可求出命题P为真命题时x的取值范围,解分式不等式可求出命题q为真命题时x的取值范围,进而得到命题q为假命题时x的取值范围,结合p∧(¬q)为真命题,可得命题P为真命题且命题q为假命题,进而得到答案.
解答:解:解不等式4-2x≥0得x≤2,即命题P为真命题时x≤2
解不等式 得x<-1,即命题q为真命题时x<-1
得x<-1,即命题q为真命题时x<-1
则命题q为假命题时x≥-1
又∵p∧(¬q)为真命题
∴命题P为真命题且命题q为假命题
∴x≤2且x≥-1
故-1≤x≤2
故p∧(¬q)为真命题时x的取值范围为[-1,2]
点评:本题考查的知识点是复合命题的真假,解不等式求出命题P和命题q为真命题时x的取值范围,是解答的关键.
解答:解:解不等式4-2x≥0得x≤2,即命题P为真命题时x≤2
解不等式
 得x<-1,即命题q为真命题时x<-1
得x<-1,即命题q为真命题时x<-1则命题q为假命题时x≥-1
又∵p∧(¬q)为真命题
∴命题P为真命题且命题q为假命题
∴x≤2且x≥-1
故-1≤x≤2
故p∧(¬q)为真命题时x的取值范围为[-1,2]
点评:本题考查的知识点是复合命题的真假,解不等式求出命题P和命题q为真命题时x的取值范围,是解答的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
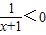 ,若p∧(¬q)为真命题,求x的取值范围.
,若p∧(¬q)为真命题,求x的取值范围.