题目内容
如图，四棱锥P－ABCD的底面ABCD是平行四边形，M、N分别是AB、PC的中点，且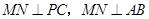
.证明：平面PAD⊥平面PDC.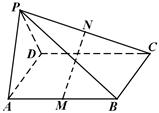
【答案】
设PD中点为H，连接NH、AH，则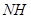
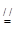
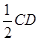，所以
，
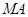
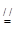
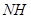
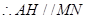
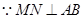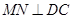，故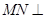
平面PCD，故
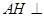平面PCD，平面PAD⊥平面PDC
【解析】
试题分析：设PD中点为H，连接NH、AH，则NH是三角形PCD的中位线，，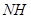
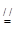
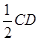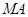
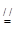
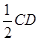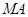
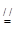
而，故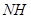，四边形AMNH为平行四边形，.
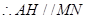而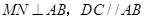
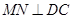，故，又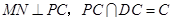
，
故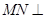平面PCD，而
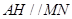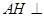，故平面PCD，
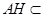平面PAD，故平面PAD⊥平面PDC.
考点：面面垂直的判定
点评：要证两面垂直，根据判定定理只需在其中一个平面内存在一条直线垂直于另外一面，转化为证明线面垂直，进而结合线面垂直的判定转化为证明线线垂直
练习册系列答案
相关题目
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，CE∥AB．
如图，四棱锥P-ABCD的底面ABCD是正方形，AC∩BD=O，PA⊥底面ABCD，OE⊥PC于E．
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，且PA=AB=1，
如图，四棱锥P-ABCD中，底面ABCD为矩形，PD⊥平面ABCD，点E，F分别是AB和PC的中点．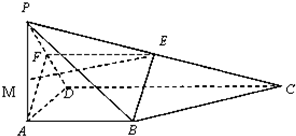
如图，四棱锥P-ABCD，PA⊥底面ABCD，AB∥CD，AB⊥AD，AB=AD=