题目内容
已知点P是直角坐标平面内的动点,点P到直线 的距离为d1,到点F(–
1,0)的距离为d2,且
的距离为d1,到点F(–
1,0)的距离为d2,且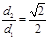 .
.
(1) 求动点P所在曲线C的方程;
(2)
直线 过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线
过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线 的垂线,对应的垂足分别为
的垂线,对应的垂足分别为 ,试判断点F与以线段
,试判断点F与以线段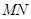 为直径的圆的位置关系(指在圆内、圆上、圆外等情况);
为直径的圆的位置关系(指在圆内、圆上、圆外等情况);
(3)
记 ,
, ,
, (A、B、
(A、B、 是(2)中的点),问是否存在实数
是(2)中的点),问是否存在实数 ,使
,使 成立.若存在,求出
成立.若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】
20.(1) 设动点为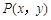
依据题意,有 ,化简得
,化简得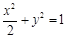 .
.
即为动点P所在曲线C的方程。·························································· 3分
(2) 点F在以MN为直径的圆的外部.
 理由:由题意可知,当过点F的直线
理由:由题意可知,当过点F的直线 的斜率为0时,不合题意,故可设直线
的斜率为0时,不合题意,故可设直线 :
: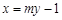 ,如图所示.联立方程组
,如图所示.联立方程组 ,可化为
,可化为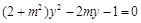 ,则点
,则点 、
、 的坐标满足
的坐标满足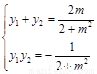 .
.
又 、
、 ,可得点
,可得点 、
、 .
.
因 ,
,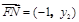 ,则
,则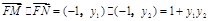 =
= .
.
于是, 为锐角,即点F在以MN为直径的圆的外部.······················· 10分
为锐角,即点F在以MN为直径的圆的外部.······················· 10分
(3) 依据 (2) 可算出 ,
, ,
,
则 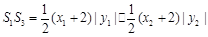
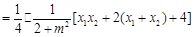
 ,
,


 .
.
所以,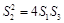 ,即存在实数
,即存在实数 使得结论成立.······························· 12分
使得结论成立.······························· 12分
【解析】略

练习册系列答案
相关题目