题目内容
已知函数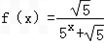 ,m为正整数.
,m为正整数.
(I)求f(1)+f(0)和f(x)+f(1﹣x)的值;
(II)若数列{an}的通项公式为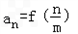 (n=1,2,…,m),求数列{an}的前m项和Sm;
(n=1,2,…,m),求数列{an}的前m项和Sm;
(III)设数列{bn}满足: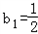 ,b n+1=bn2+bn,设
,b n+1=bn2+bn,设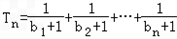 ,若(Ⅱ)中的Sm满足对任意不小于3的正整数n,
,若(Ⅱ)中的Sm满足对任意不小于3的正整数n,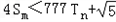 恒成立,试求m的最大值.
恒成立,试求m的最大值.
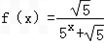 ,m为正整数.
,m为正整数.(I)求f(1)+f(0)和f(x)+f(1﹣x)的值;
(II)若数列{an}的通项公式为
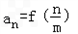 (n=1,2,…,m),求数列{an}的前m项和Sm;
(n=1,2,…,m),求数列{an}的前m项和Sm;(III)设数列{bn}满足:
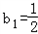 ,b n+1=bn2+bn,设
,b n+1=bn2+bn,设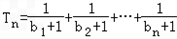 ,若(Ⅱ)中的Sm满足对任意不小于3的正整数n,
,若(Ⅱ)中的Sm满足对任意不小于3的正整数n,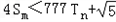 恒成立,试求m的最大值.
恒成立,试求m的最大值.解:(Ⅰ) =1;
=1;
f(x)+f(1﹣x)= =
= =1;
=1;
(Ⅱ)由(Ⅰ)得 ,即
,即 =1,
=1,
∴ak+a m﹣k=1,
由Sm=a1+a2+a3+...+a m﹣1+am,①
得Sm=a m﹣1+a m﹣2+a m﹣3+...+a1+am,②
由①+②,得2Sm=(m﹣1)×1+2am,
∴ ,
,
(Ⅲ)∵ ,b n+1=bn2+bn=bn(b n+1),
,b n+1=bn2+bn=bn(b n+1),
∴对任意的n∈N*,bn>0.
∴ ,即
,即 .
.
∴ +…+
+…+ .
.
∵b n+1﹣bn=bn2>0,
∴b n+1>bn,∴数列{bn}是单调递增数列.
∴Tn关于n递增.当n≥3,且n∈N+时,Tn≥T3.∵
∴ .
.
∴ ,
,
∴m<650. 5,而m为正整数,
∴m的最大值为650.
 =1;
=1;f(x)+f(1﹣x)=
 =
= =1;
=1;(Ⅱ)由(Ⅰ)得
 ,即
,即 =1,
=1,∴ak+a m﹣k=1,
由Sm=a1+a2+a3+...+a m﹣1+am,①
得Sm=a m﹣1+a m﹣2+a m﹣3+...+a1+am,②
由①+②,得2Sm=(m﹣1)×1+2am,
∴
 ,
,(Ⅲ)∵
 ,b n+1=bn2+bn=bn(b n+1),
,b n+1=bn2+bn=bn(b n+1),∴对任意的n∈N*,bn>0.
∴
 ,即
,即 .
.∴
 +…+
+…+ .
.∵b n+1﹣bn=bn2>0,
∴b n+1>bn,∴数列{bn}是单调递增数列.
∴Tn关于n递增.当n≥3,且n∈N+时,Tn≥T3.∵

∴
 .
.∴
 ,
,∴m<650. 5,而m为正整数,
∴m的最大值为650.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
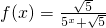 ,m为正整数.
,m为正整数.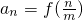 (n=1,2,…,m),求数列{an}的前m项和Sm;
(n=1,2,…,m),求数列{an}的前m项和Sm;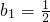 ,bn+1=bn2+bn,设
,bn+1=bn2+bn,设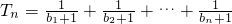 ,若(Ⅱ)中的Sm满足对任意不小于3的正整数n,
,若(Ⅱ)中的Sm满足对任意不小于3的正整数n,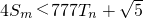 恒成立,试求m的最大值.
恒成立,试求m的最大值.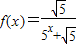 ,m为正整数.
,m为正整数.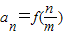 (n=1,2,…,m),求数列{an}的前m项和Sm;
(n=1,2,…,m),求数列{an}的前m项和Sm; ,bn+1=bn2+bn,设
,bn+1=bn2+bn,设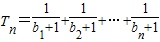 ,若(Ⅱ)中的Sm满足对任意不小于3的正整数n,
,若(Ⅱ)中的Sm满足对任意不小于3的正整数n,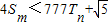 恒成立,试求m的最大值.
恒成立,试求m的最大值.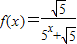 ,m为正整数.
,m为正整数.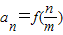 (n=1,2,…,m),求数列{an}的前m项和Sm;
(n=1,2,…,m),求数列{an}的前m项和Sm;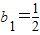 ,bn+1=bn2+bn,设
,bn+1=bn2+bn,设 ,若(Ⅱ)中的Sm满足对任意不小于3的正整数n,
,若(Ⅱ)中的Sm满足对任意不小于3的正整数n,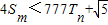 恒成立,试求m的最大值.
恒成立,试求m的最大值.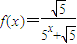 ,m为正整数.
,m为正整数.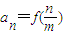 (n=1,2,…,m),求数列{an}的前m项和Sm;
(n=1,2,…,m),求数列{an}的前m项和Sm;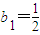 ,bn+1=bn2+bn,设
,bn+1=bn2+bn,设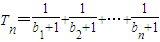 ,若(Ⅱ)中的Sm满足对任意不小于3的正整数n,
,若(Ⅱ)中的Sm满足对任意不小于3的正整数n,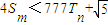 恒成立,试求m的最大值.
恒成立,试求m的最大值.