题目内容
数列
的前
项和记为
，
．
（Ⅰ）求的通项公式；
（Ⅱ）等差数列
的各项为正，其前项和为
且
,又
成等比数列．求的通项公式；
解：（Ⅰ）由
，得
，两式相减得
，
所以
--------------------2分
所以
-----------3分
又
所以
，
从而
--------------5分
而
，不符合上式，
所以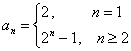
--------------6分
（Ⅱ）（1）因为为等差数列，且前三项的和，所以
，--------7分
可设
由于
，因为成等比数列．
所以
所以
---------------------12分
练习册系列答案
阅读快车系列答案
相关题目
的前
项和记为
，
，
．
为何值时，数列
的前
有最大值，且
，又
成等比数列，求
．
等比数列,其中
成等差数列.
的通项公式;
项和记为
证明: 
…).
的前
项和记为
,
,点
在直线
上,
．
为何值时,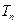数列
,
是数列
的前
的值．
的前
项和记为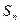
，
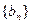的各项为正，其前
,且
，
的前
项和记为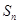
，
，
．
为何值时，数列
的前
有最大值，且
，又
，
，
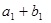成等比数列，求
．