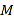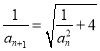题目内容
【题目】在![]() 中,已知
中,已知![]() ,M是BC的中点.
,M是BC的中点.
(1)若![]() ,求向量
,求向量![]() 与向量
与向量![]() 的夹角的余弦值;
的夹角的余弦值;
(2)若O是线段AM上任意一点,且![]() ,求
,求![]() 的最小值;
的最小值;
(3)若点P是边BC上的一点,且![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用向量夹角公式即可求出向量![]() 与向量
与向量![]() 的夹角的余弦值;
的夹角的余弦值;
(2)根据已知条件求出线段AM的长,利用平行四边形法则得到,![]() ,
,
![]() 表示成关于
表示成关于![]() 的二次函数,求二次函数的最小值,即可求出结果;
的二次函数,求二次函数的最小值,即可求出结果;
(3)先用数量积定义把![]() 转化为
转化为![]() 的三角函数的表达式,再利用基本不等式求
的三角函数的表达式,再利用基本不等式求![]() 的最小值,从而得所求.
的最小值,从而得所求.
(1)设向量![]() 与向量
与向量![]() 的夹角为
的夹角为![]() ,
,
由,![]()
(![]() )
)![]() ,
,
![]() =
=![]()
![]()
![]() ,同理
,同理![]()
![]() ,
,
![]() 向量
向量![]() 与向量
与向量![]() 的夹角的余弦值
的夹角的余弦值![]() .
.
(2)![]()
![]() ,设
,设![]() ,
,
则![]() ,而
,而![]() ,
,
![]() =
=![]()
=![]() =
=![]()
当![]() 时,
时,![]() 的最小值是
的最小值是![]() ;
;
(3)设![]() ,则
,则![]()
![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
当且仅当![]() 时,等号成立,
时,等号成立,
![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目