题目内容
（2012•卢湾区一模）已知| a |
| b |
（1）设
| OA |
| a |
| OB |
| b |
| OC |
| 1 |
| 3 |
| a |
| b |
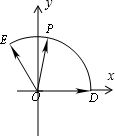
（2）如图，若
| a |
| OD |
| b |
| OE |
| a |
| b |
| a |
| b |
 |
| DE |
| OP |
| OD |
| OE |
分析：（1）利用向量共线定理，及已知向量建立等式，利用平面向量基本定理，即可得到结论；
（2）建立坐标系，用三角函数确定x+y，再利用辅助角公式，即可得到结论．
（2）建立坐标系，用三角函数确定x+y，再利用辅助角公式，即可得到结论．
解答：解：（1）由题意，A、B、C三点共线，可设
=k
，（2分）
∵
=
，
=t
（t∈R），
=
(
+
)，
∴
=t
-
，
=
+(
-t)
，
∴t
-
=
+k(
-t)
∴k=-3，t=
．（6分）
（2）以O为原点，OD为x轴建立直角坐标系，则D（1，0），E（-
，
）．
设∠POD=α（0≤α≤
π），则P（cosα，sinα），由
=x
+y
，得cosα=x-
y，sinα=
y，于是y=
sinα，x=cosα+
sinα，（10分）
于是x+y=cosα+
sinα=2sin（α+
），
故当α=
时，x+y的最大值为2．（14分）
| AB |
| BC |
∵
| OA |
| a |
| OB |
| b |
| OC |
| 1 |
| 3 |
| a |
| b |
∴
| AB |
| b |
| a |
| BC |
| 1 |
| 3 |
| a |
| 1 |
| 3 |
| b |
∴t
| b |
| a |
| k |
| 3 |
| a |
| 1 |
| 3 |
| b |
∴k=-3，t=
| 1 |
| 2 |
（2）以O为原点，OD为x轴建立直角坐标系，则D（1，0），E（-
| 1 |
| 2 |
| ||
| 2 |
设∠POD=α（0≤α≤
| 2 |
| 3 |
| OP |
| OD |
| OE |
| 1 |
| 2 |
| ||
| 2 |
| 2 | ||
|
| 1 | ||
|
于是x+y=cosα+
| 3 |
| π |
| 6 |
故当α=
| π |
| 3 |
点评：本题考查向量知识的综合运用，考查三角函数知识，解题的关键是掌握向量共线定理，正确运用三角函数知识，属于中档题．
练习册系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目