题目内容
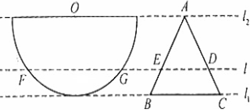
 如图:l1,l2,l3,l4是同一平面内的四条平行直线,且每相邻的两条平行直线间的距离都是h,正方形ABCD的四个顶点分别在这四条直线上,且正方形的边长为5,则h=( )
如图:l1,l2,l3,l4是同一平面内的四条平行直线,且每相邻的两条平行直线间的距离都是h,正方形ABCD的四个顶点分别在这四条直线上,且正方形的边长为5,则h=( )分析:根据正方形的边长,得到AE,AB的长,根据勾股定理得到BE的长,△ABE的面积是长方形的面积的
,再根据三角形的面积等于
BE•h就可以求出h的长.
| 1 |
| 4 |
| 1 |
| 2 |
解答: 解:过A点作AH⊥BE于H点.
解:过A点作AH⊥BE于H点.
∵S△ABE=S△FBE=S△EDF=S△CDF,
又∵正方形ABCD的面积是25,
∴S△ABE=
,且AB=AD=5,(7分)
又∵l1∥l2∥l3∥l4,
∴E、F分别是AD与BC的中点,
∴AE=
AD=
,
∴在Rt△ABE中,
BE=
=
,(10分)
又∵AB•AE=BE•AH,
∴AH=
=
=
.(12分)
故选C.
 解:过A点作AH⊥BE于H点.
解:过A点作AH⊥BE于H点.∵S△ABE=S△FBE=S△EDF=S△CDF,
又∵正方形ABCD的面积是25,
∴S△ABE=
| 25 |
| 4 |
又∵l1∥l2∥l3∥l4,
∴E、F分别是AD与BC的中点,
∴AE=
| 1 |
| 2 |
| 5 |
| 2 |
∴在Rt△ABE中,
BE=
| AB2+AE2 |
5
| ||
| 2 |
又∵AB•AE=BE•AH,
∴AH=
| AB•AE |
| BE |
5×
| ||||
|
| 5 |
故选C.
点评:本题考查进行简单的演绎推理、正方形的性质和勾股定理,根据三角形的面积公式得到四个三角形的面积相等是解决本题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
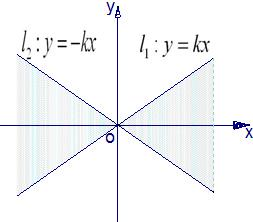 如图,直线l1:y=kx(k>0)与直线l2:y=-kx之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.
如图,直线l1:y=kx(k>0)与直线l2:y=-kx之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2. 已知二次函数f(x)=3x2-3x直线l1:x=2和l2:y=3tx,其中t为常数且0<<1.直线l2与函数f(x)的图象以及直线l1、l2与函数f(x)的图象围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为S(t).
已知二次函数f(x)=3x2-3x直线l1:x=2和l2:y=3tx,其中t为常数且0<<1.直线l2与函数f(x)的图象以及直线l1、l2与函数f(x)的图象围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为S(t).