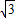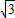题目内容
已知圆锥的高为1,轴截面顶角为120°时,过圆锥顶点的截面中,最大截面面积为( )
分析:作出过圆锥顶点的截面,设出底面圆心到截面底边的距离x,把截面面积用x表示,然后利用基本不等式求其最值.
解答: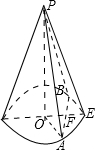 解:如图,过圆锥顶点P认作一截面PAB,交底面圆与AB,过O作AB的垂线OF,垂足为F,交底面圆周与E,
解:如图,过圆锥顶点P认作一截面PAB,交底面圆与AB,过O作AB的垂线OF,垂足为F,交底面圆周与E,
因为圆锥轴截面的顶角为120°,则∠OPE=60°,又圆锥PO的高PO=1,在直角三角形POE中,有OE=tan60°=
,
即圆锥底面半径为3,所以OA=OE=
,设OF=x,则AF=
=
,
在直角三角形POF中,PF=
=
,
所以,S△PAB=
AB•PF=AF•PF=
•
≤
=2.
当且仅当3-x2=1+x2,即x=1时“=”成立.
所以,过圆锥顶点的截面中,最大截面面积为2.
故选C.
 解:如图,过圆锥顶点P认作一截面PAB,交底面圆与AB,过O作AB的垂线OF,垂足为F,交底面圆周与E,
解:如图,过圆锥顶点P认作一截面PAB,交底面圆与AB,过O作AB的垂线OF,垂足为F,交底面圆周与E,因为圆锥轴截面的顶角为120°,则∠OPE=60°,又圆锥PO的高PO=1,在直角三角形POE中,有OE=tan60°=
| 3 |
即圆锥底面半径为3,所以OA=OE=
| 3 |
(
|
| 3-x2 |
在直角三角形POF中,PF=
| 12+x2 |
| 1+x2 |
所以,S△PAB=
| 1 |
| 2 |
| 3-x2 |
| 1+x2 |
| (3-x2)+(1+x2) |
| 2 |
当且仅当3-x2=1+x2,即x=1时“=”成立.
所以,过圆锥顶点的截面中,最大截面面积为2.
故选C.
点评:本题考查了棱锥的结构特征,考查了利用基本不等式求最值,学生解答此题时容易出错,往往不假思索的认为截面积最大的是轴截面,该题是否是轴截面面积最大取决于轴截面的顶角,此题是基础题.

练习册系列答案
相关题目
 的正三角形,O是底面圆心.
的正三角形,O是底面圆心.
 的中点
的中点 作平行于圆锥底面的截面,求截得的圆台的体积.
作平行于圆锥底面的截面,求截得的圆台的体积.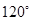 时,过圆锥顶点的截面中,最大截面面积为( )
时,过圆锥顶点的截面中,最大截面面积为( )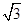 B、
B、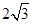 C、2
D、1
C、2
D、1