题目内容
设a＞0，a≠1，函数f（x）=ax+2|sin2πx|-2（x＞0）有四个零点，则a的值为 ．
分析：由题意可得函数y=ax-2的图象（蓝线）和函数y=-2|sin2πx|的图象（红线）有4个交点，把点（1，0）代入y=ax-2，求得a的值．
解答：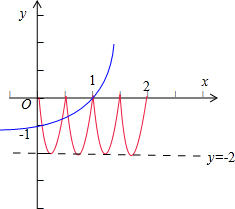
解：根据函数f（x）=ax+2|sin2πx|-2（x＞0）有四个零点，
可得函数y=ax-2的图象（绿线）和函数y=-2|sin2πx|的图象（红线）有4个交点，
如图所示：
根据函数y=ax-2的图象（蓝线）经过点（0，-1）、（1，0），
可得a1-2=0，
解得 a=2，
故答案为：2．
解：根据函数f（x）=ax+2|sin2πx|-2（x＞0）有四个零点，可得函数y=ax-2的图象（绿线）和函数y=-2|sin2πx|的图象（红线）有4个交点，
如图所示：
根据函数y=ax-2的图象（蓝线）经过点（0，-1）、（1，0），
可得a1-2=0，
解得 a=2，
故答案为：2．
点评：本题主要考查函数的零点的个数判断，体现了转化以及数形结合的数学思想，属于中档题．
练习册系列答案
综合自测系列答案
相关题目
的定义域为R，若存在与
无关的正常数M，使
对一切实数
；
；
；
．其中是“有界泛函”的个数为 （ ）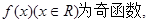
（ ）
D．5
的定义域为R，若存在与
无关的正常数M，使
对一切实数
；
；
；
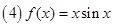．其中是“有界泛函”的个数为 （ ）
)的定义域为R，若存在与
对一切实数
②f(
④
其中是“有界泛函”的个数为（
）
对一切实数x均成立，则称f(x)为“有界泛函”，给出以下函数：①f(x) =x2，②f(x)=2x，③
其中是“有界泛函”的个数为