Question

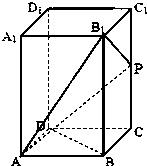如图，在长方体ABCD-A₁B₁C₁D₁中，AA₁=2AB=2AD，且

PC1

=λ

CC1

（0＜λ＜1）．
（Ⅰ）求证：对任意0＜λ＜1，总有AP⊥BD；
（Ⅱ）若λ=

1

3

，求二面角P-AB₁-B的余弦值；
（Ⅲ）是否存在λ，使得AP在平面B₁AC上的射影平分∠B₁AC？若存在，求出λ的值，若不存在，说明理由．

Answer 1

分析：（I）以D为原点，建立如图所示空间直角坐标系，设AB=1可得D、A、C、B₁、C₁、P各点的坐标，从而得到向量

BD

、

AP

的坐标，算出

BD

•

AP

=0可得

BD

⊥

AP

，即对任意0＜λ＜1总有AP⊥BD；
（II）利用空间向量数量积为零的方法，建立方程组解出平面AB₁P的一个法向量为

n

=(1，3，-

3

2

)，结合平面ABB₁的一个法向量为

m

=(1，0，0)，利用空间向量的夹角公式算出

m

、

n

夹角的余弦，即可得到二面角P-AB₁-B的余弦值；
（III）由题结合图形，可得当

AP

分别与

AC

、

AB1

所成的角相等时，即存在实数λ满足条件，由此建立向量关系式，化简可得关于λ的方程，解之得λ=

5- 10

4

∈(0，1)．由此可得存在满足题意的实数λ，使得AP在平面B₁AC上的射影平分∠B₁AC．

解答：解：（I）以D为原点，分别以DA、DC、DD₁所在直线为x、y、z轴，建立空间直角坐标系，如图所示
设AB=1，则可得D（0，0，0），A（1，0，0），C（0，1，0），
B₁（1，1，2），C₁（0，1，2），P（0，1，2-2λ）
∴

BD

=(-1，-1，0)，

AP

=(-1，1，2-2λ)
可得

BD

•

AP

=-1×(-1)+(-1)×1+0=0
∴

BD

⊥

AP

，即对任意0＜λ＜1，总有AP⊥BD；…（4分）
（II）由（I）及λ=

1

3

，得

AP

=(-1，1，

4

3

)，

AB1

=(0，1，2)
设平面AB₁P的一个法向量为

n

=(1，x，y)
可得

n • AP =-1+x+ 4 3 y=0 n • AB1 =x+2y=0

，解之得

x=3 y=- 3 2

∴平面AB₁P的一个法向量为

n

=(1，3，-

3

2

)，
又∵平面ABB₁的一个法向量为

m

=(1，0，0)，
∴设二面角P-AB₁-B的大小为θ，可得cosθ=|

m • n

| m |•| n |

|=

2

7

因此可得二面角P-AB₁-B的余弦值为

2

7

…（9分）
（III） 假设存在实数λ（0＜λ＜1）满足条件，
由题结合图形，只需满足

AP

分别与

AC

、

AB1

所成的角相等，
即 

AP • AC

| AP |•| AC |

=

AP • AB1

| AP |•| AB1 |

，约去|

AP

|有

2

2

=

5-4λ

5

，
解得 λ=

5- 10

4

∈(0，1)．
所以存在满足题意的实数λ=

5- 10

4

，使得AP在平面B₁AC上的射影平分∠B₁AC．…（14分）

点评：本题在正四棱柱中求证线线垂直、并求二面角的大小．着重考查了正棱柱的性质、利用空间向量研究二面角和直线与平面所成角等知识，属于中档题．