题目内容
函数f（x）=x2-3mx+n在[-2，+∞）上是增函数，则m的取值范围是________．
（-∞，-
]
分析：由函数f（x）=x2-3mx+n是开口向上，对称轴为x=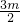
的抛物线，且函数f（x）=x2-3mx+n在[-2，+∞）上是增函数，知
，由此能求出实数m的取值范围．
解答：∵函数f（x）=x2-3mx+n是开口向上，对称轴为x=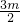的抛物线，
且函数f（x）=x2-3mx+n在[-2，+∞）上是增函数，
∴，解得m
．
故答案为：（-∞，-]．
点评：本题考查二次函数的性质和应用，是基础题．解题时要认真审题，仔细解答．
]分析：由函数f（x）=x2-3mx+n是开口向上，对称轴为x=
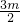的抛物线，且函数f（x）=x2-3mx+n在[-2，+∞）上是增函数，知，由此能求出实数m的取值范围．解答：∵函数f（x）=x2-3mx+n是开口向上，对称轴为x=
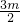的抛物线，且函数f（x）=x2-3mx+n在[-2，+∞）上是增函数，
∴
，解得m．故答案为：（-∞，-
]．点评：本题考查二次函数的性质和应用，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
相关题目