题目内容

设抛物线y²=2px（p＞0）的焦点为F，点M在抛物线上，线段MF的延长线与直线 $数学公式$ 交与点N，则 $数学公式$ =________．

$\text{[math]}$
分析：如图所示．过点M作MQ⊥l交于点Q，由抛物线的定义可得|MF|=|MQ|．由MQ∥FR，可得 $\text{[math]}$ ，通过化简代入即可得出．
解答：如图所示．过点M作MQ⊥l交于点Q．

由抛物线的定义可得|MF|=|MQ|．
设∠FMQ=θ，∵MQ∥FR，∴∠NFR=∠FMQ=θ．
∴在直角△NMQ、△RFN中， $\text{[math]}$ ．
∴ $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ．
故答案为 $\text{[math]}$ ．
点评：熟练掌握抛物线的定义性质、平行线分线段成比例定理及其直角三角形的边角关系即可得出．

练习册系列答案

新课程寒暑假练习丛书暑假园地中国地图出版社系列答案

高效A计划期末寒假衔接中南大学出版社系列答案

智乐文化暑假作业期末综合复习东南大学出版社系列答案

智趣暑假作业云南科技出版社系列答案

少年智力开发报期末复习暑假作业系列答案

金象教育U计划学期系统复习暑假作业系列答案

八斗才火线计划暑假西安交通大学出版社系列答案

Happy暑假作业快乐暑假武汉大学出版社系列答案

赢在假期期末加暑假合肥工业大学出版社系列答案

暑假作业阅读与写作好帮手长江出版社系列答案

相关题目

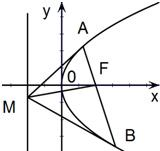设抛物线y²=2px（p＞0）的焦点为F，经过点F的直线交抛物线于A，B两点，且A，B两点坐标分别为（x₁，y₁）、（x₂，y₂），y₁＞0，y₂＜0，M是抛物线的准线上的一点，O是坐标原点．若直线MA，MF，MB的斜率分别记为：K_MA=a，K_MF=b，K_MB=c，（如图）
（I）若y₁y₂=-4，求抛物线的方程；
（II）当b=2时，求a+c的值；
（III）如果取KMA=2，KMB=-

时，判定|∠AMF-∠BMF|和∠MFO的值大小关系．并说明理由．

7、设抛物线y²=2px（p＞0）上一点A（1，2）到点B（x₀，0）的距离等于到直线x=-1的距离，则实数x₀的值是

抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形，阿基米德三角形有一些有趣的性质，如：若抛物线的弦过焦点，则过弦的端点的两条切线的交点在其准线上．设抛物线y²=2px（p＞0），弦AB过焦点，△ABQ为阿基米德三角形，则△ABQ为（　　）

A．锐角三角形

B．直角三角形

C．钝角三角形

D．随Q位置变化前三种情况都有可能

设抛物线y²=2px（p＞0）的焦点为F，其准线与x轴的交点为Q，过Q点的直线l交抛物线于A，B两点．
（1）若直线l的斜率为

=0；
（2）设直线FA，FB的斜率分别为k₁，k₂，求k₁+k₂的值．

抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形，阿基米德三角形有一些有趣的性质，如：若抛物线的弦过焦点，则过弦的端点的两条切线的交点在其准线上．设抛物线y²=2px（p＞0），弦AB过焦点，△ABQ为其阿基米德三角形，则△ABQ的面积的最小值为（　　）