题目内容
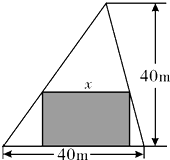在如图所示的锐角三角形空地中，欲建一个面积最大的内接矩形花园（阴影部分），则其边长x为（ ）分析：设矩形高为y，由三角形相似可求得40=x+y结合x＞0，y＞0，x＜40，y＜40，利用基本不等式即可求得答案．
解答：解：设矩形高为y，由三角形相似得：
=
，
且x＞0，y＞0，x＜40，y＜40，变形可得x+y=40
故矩形的面积S=xy≤(
)2=400
当且仅当x=y=20m时，取等号，
故选D
| x |
| 40 |
| 40-y |
| 40 |
且x＞0，y＞0，x＜40，y＜40，变形可得x+y=40
故矩形的面积S=xy≤(
| x+y |
| 2 |
当且仅当x=y=20m时，取等号，
故选D
点评：本题考查函数的最值，基本不等式，考查相似三角形的应用，求得40=x+y是关键，属中档题．
练习册系列答案
相关题目
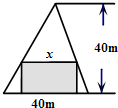（2013•陕西）在如图所示的锐角三角形空地中，欲建一个面积最大的内接矩形花园（阴影部分），则其边长x为
（2013•陕西）在如图所示的锐角三角形空地中，欲建一个面积不小于300m2的内接矩形花园（阴影部分），则其边长x（单位m）的取值范围是（ ）
在如图所示的锐角三角形空地中，欲建一个面积不小于300m2的内接矩形花园（阴影部分），则其边长x（单位m）的取值范围是
在如图所示的锐角三角形空地中，欲建一个面积最大的内接矩形花园（阴影部分），其边长为x，面积为s（x）．