题目内容
若定义在R上的偶函数f(x)在(-∞,0]上是增函数,且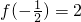 ,那么不等式
,那么不等式 在
在 上的解集为
上的解集为
- A.[-
 ,-
,- )∪(-
)∪(- ,
, )∪(
)∪( ,
, ]
] - B.[-
 ,-
,- )∪(
)∪( ,
, ]
] - C.[-
 ,-
,- )∪(-
)∪(- ,
, )
) - D.[-
 ,-
,- )∪(-
)∪(- ,
, )∪(
)∪( ,
, ]
]
D
分析:利用偶函数的图象关于y轴对称,又且在(-∞,0]上为增函数,将不等式中的抽象的对应法则“f”化去,变形为三角不等式,求出解集.
解答:∵f(x)是定义在R上的偶函数,且在(-∞,0]上为增函数,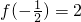 ,
, ∴原不等式可化为
∴原不等式可化为 或
或 
∵x∈ ∴2x-
∴2x- ∈[
∈[ ],∴须2x-
],∴须2x- ∈[
∈[ )∪(
)∪( )∪(
)∪( ],解得x∈[
],解得x∈[ )∪(
)∪( )∪(
)∪( ]
]
故选D
点评:本题主要考查函数的奇偶性、单调性及其应用,三角不等式的解法.
分析:利用偶函数的图象关于y轴对称,又且在(-∞,0]上为增函数,将不等式中的抽象的对应法则“f”化去,变形为三角不等式,求出解集.
解答:∵f(x)是定义在R上的偶函数,且在(-∞,0]上为增函数,
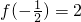 ,
, ∴原不等式可化为
∴原不等式可化为 或
或 
∵x∈
 ∴2x-
∴2x- ∈[
∈[ ],∴须2x-
],∴须2x- ∈[
∈[ )∪(
)∪( )∪(
)∪( ],解得x∈[
],解得x∈[ )∪(
)∪( )∪(
)∪( ]
]故选D
点评:本题主要考查函数的奇偶性、单调性及其应用,三角不等式的解法.

练习册系列答案
相关题目
若定义在R上的偶函数f(x)和奇函数g(x)满足f(x)+g(x)=ex,则g(x)=( )
| A、ex-e-x | ||
B、
| ||
C、
| ||
D、
|
若定义在R上的偶函数f(x)在(-∞,0]上是增函数,且f(-
)=2,那么不等式f(sin(2x-
))<2在[-
,
]上的解集为( )
| 1 |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
A、[-
| ||||||||||||
B、[-
| ||||||||||||
C、[-
| ||||||||||||
D、[-
|
若定义在R上的偶函数f(x)满足f(x+1)=-f(x),且在区间[0,1]上单调递减,则( )
A、f(2)<f(
| ||
B、f(1)<f(2)<f(
| ||
C、f(
| ||
D、f(1)<f(
|