题目内容
已知函数f(x)=kx+b(k≠0)的图象与x、y轴分别相交于点A、B两点,向量 =(2,2),又函数g(x)=x2-x-6,且y=g(x)+m的值域是[0,+∞).
=(2,2),又函数g(x)=x2-x-6,且y=g(x)+m的值域是[0,+∞).
(1)求k,b及m的值;
(2)当x满足f(x)>g(x)时,求函数 的最小值.
的最小值.
解:(1)∵函数f(x)=kx+b(k≠0)的图象与x、y轴分别相交于点A、B两点,
∴ ,B(0,b),∴
,B(0,b),∴ .
.
∵向量 =(2,2),∴
=(2,2),∴ ,解得
,解得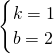 .
.
∵函数g(x)=x2-x-6+m的值域是[0,+∞),
∴△=1-4(m-6)=0,解得m= .
.
(2)由(1)可知:f(x)=x+2,
∵f(x)>g(x),∴x+2>x2-x-6,
化为x2-2x-8<0,∴(x-4)(x+2)<0,∴-2<x<4.
∴函数 =
= =(x+2)
=(x+2) -1,
-1,
∵0<x+2<6,∴
 =4,当且仅当x+2=2,即x=0时等号成立,
=4,当且仅当x+2=2,即x=0时等号成立,
∴x=0时, 的最小值是3.
的最小值是3.
分析:(1)先求出点A、B的坐标,根据向量相等即可求出k,b;根据二次函数的判别式与值域的关系即可求出m;
(2)利用基本不等式的性质即可求出.
点评:熟练掌握向量相等、二次函数的性质及基本不等式的性质是解题的关键.
∴
 ,B(0,b),∴
,B(0,b),∴ .
.∵向量
 =(2,2),∴
=(2,2),∴ ,解得
,解得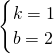 .
.∵函数g(x)=x2-x-6+m的值域是[0,+∞),
∴△=1-4(m-6)=0,解得m=
 .
.(2)由(1)可知:f(x)=x+2,
∵f(x)>g(x),∴x+2>x2-x-6,
化为x2-2x-8<0,∴(x-4)(x+2)<0,∴-2<x<4.
∴函数
 =
= =(x+2)
=(x+2) -1,
-1,∵0<x+2<6,∴

 =4,当且仅当x+2=2,即x=0时等号成立,
=4,当且仅当x+2=2,即x=0时等号成立,∴x=0时,
 的最小值是3.
的最小值是3.分析:(1)先求出点A、B的坐标,根据向量相等即可求出k,b;根据二次函数的判别式与值域的关系即可求出m;
(2)利用基本不等式的性质即可求出.
点评:熟练掌握向量相等、二次函数的性质及基本不等式的性质是解题的关键.

练习册系列答案
相关题目