题目内容
函数y=5sinx+cos2x的最大值是________．
4
分析：利用倍角公式化cos2x为sinx，然后把函数看做关于sinx的二次函数，求出最大值．
解答：y=5sinx+cos2x=5sinx+1-2sin2x=-2（sinx-
）2+
．
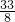∴sinx=1时，ymax=4．
故答案为：4
点评：本题考查复合三角函数的最值问题，考查学生转化思想，是中档题．
分析：利用倍角公式化cos2x为sinx，然后把函数看做关于sinx的二次函数，求出最大值．
解答：y=5sinx+cos2x=5sinx+1-2sin2x=-2（sinx-
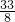）2+．∴sinx=1时，ymax=4．
故答案为：4
点评：本题考查复合三角函数的最值问题，考查学生转化思想，是中档题．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目