题目内容
【题目】已知椭圆![]() ,若在
,若在![]() ,
,![]() ,
, ,
, 四个点中有3个在
四个点中有3个在![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 与点
与点![]() 是椭圆
是椭圆![]() 上关于原点对称的两个点,且
上关于原点对称的两个点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() .(2)
.(2) ![]()
【解析】
(1) 由于椭圆是对称图形,得点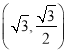 ,
,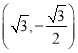 必在椭圆上,故
必在椭圆上,故![]() ,再分别讨论
,再分别讨论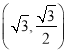 在
在![]() 上时和
上时和![]() 在
在![]() 上时椭圆的方程,根据题意进行排除,最后求解出结果。
上时椭圆的方程,根据题意进行排除,最后求解出结果。
(2) 设![]() ,
,![]() ,利用向量的坐标运算表达出
,利用向量的坐标运算表达出![]() 的值,根据对称性分类讨论设出直线
的值,根据对称性分类讨论设出直线![]() 的方程,联立椭圆方程,结合韦达定理,将
的方程,联立椭圆方程,结合韦达定理,将![]() 转化为求函数的值域问题,从而求解出
转化为求函数的值域问题,从而求解出![]() 的范围。
的范围。
解:(1)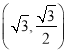 与
与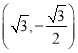 关于
关于![]() 轴对称,
轴对称,
由题意知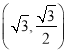 在
在![]() 上,当
上,当![]() 在
在![]() 上时,
上时,![]() ,
,![]() ,
,![]() ,
,
当![]() 在
在![]() 上时,
上时,![]() ,
,![]() ,
,
∴![]() 与
与![]() 矛盾,∴椭圆
矛盾,∴椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
,![]() ,
,![]() 、
、![]() 关于坐标原点
关于坐标原点![]() 对称,
对称,
![]() ,
,![]() ,
,
![]() .
.
当![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]() ,
,
代入椭圆方程![]() 得
得![]() ,
,![]() ,
,
![]() ,
,
由于![]() 可以取任何实数,故
可以取任何实数,故![]() .
.
当![]() 与
与![]() 轴垂直时,
轴垂直时,![]() ,
,![]() ,
,
∴![]() .
.
综上可得![]() .
.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目


