Question

若关于x的不等式(m²+4m-5)x²-4(m-1)x+3＞0对一切实数x恒成立,求m的取值范围.

Answer 1

解：m²+4m-5=0得m=-5或m=1.

(1)当m=1时原不等式变为3＞0对x∈R恒成立,故m=1;

(2)当m=-5时原不等式变为24x+3＞0,解集为{x|x＞-}≠R,不合题意,即m≠-5;

(3)当m≠1且m≠-5时,m²+4m-5≠0,一元二次不等式(m²+4m-5)x²-4(m-1)x+3＞0解集为R

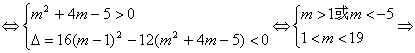1＜m＜19.

∴总之,1≤m＜19.