题目内容
在平面直角坐标系xOy中，已知过点(1，| 3 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
（1）求椭圆C的标准方程；
（2）若点B的坐标为(
| 8 |
| 5 |
3
| ||
| 5 |
（3）记M，N两点的纵坐标分别为yM，yN，试问yM•yN是否为定值？若是，请求出该定值；若不是，请说明理由．
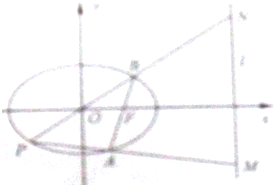
分析：（1）如图所示，由于过点(1，
)的椭圆C：
+
=1（a＞b＞0）的右焦点为F（1，0），可得
，解得即可．
（2）由点B的坐标为(
，
)，点P与点B关于坐标原点对称，可得P(-
，-
)．利用斜率计算公式可得kBF．即可得到直线BF的方程y=
(x-1)．与椭圆的方程联立解得xA．进而得到直线PA的方程．
（3）椭圆C的右准线l为：x=
=4．当直线AB⊥x轴时，B（1，
），A(1，-
)，P(-1，-
)．即可得到直线PB的方程，直线PA的方程，即可得到yM•yN．当直线AB的斜率存在时，设A（x1，y1），B（x2，y2）．则P（-x2，-y2）．可得直线PB的方程为：y=
x，与x=4联立，解得yN=
．设直线AB的方程为：y=k（x-1）．直线PA的方程为：kPA=
．由
+
=1，
+
=1，两式相减得
+
=0．得到
+kPA•kAB=0，即kPA=-
．得到直线PA的方程为：y+y2=-
(x+x2)．联立直线PA与l的方程
，解得yM．进而得到yM•yN．
| 3 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
|
（2）由点B的坐标为(
| 8 |
| 5 |
3
| ||
| 5 |
| 8 |
| 5 |
3
| ||
| 5 |
| 3 |
（3）椭圆C的右准线l为：x=
| a2 |
| c |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| y2 |
| x2 |
| 4y2 |
| x2 |
| y1+y2 |
| x1+x2 |
| ||
| 4 |
| ||
| 3 |
| ||
| 4 |
| ||
| 3 |
| (x1+x2)(x1-x2) |
| 4 |
| (y1+y2)(y1-y2) |
| 3 |
| 3 |
| 4 |
| 3 |
| 4k |
| 3 |
| 4k |
|
解答：解：（1）如图所示，
∵过点(1，
)的椭圆C：
+
=1（a＞b＞0）的右焦点为F（1，0），
∴
，解得c=1，b2=3，a2=4．
∴椭圆C的标准方程为：
+
=1．
（2）∵点B的坐标为(
，
)，点P与点B关于坐标原点对称．∴P(-
，-
)．
可得kBF=
=
．
∴直线BF的方程y=
(x-1)．
联立
，化为5x2-8x=0，解得x=0或
．
把x=0代入直线方程可得y=-
．
∴A(0，-
)．
∴kPA=
=-
．
∴直线PA的方程为：y=-
x-
．
（3）椭圆C的右准线l为：x=
=4．
①当直线AB⊥x轴时，B（1，
），A(1，-
)，P(-1，-
)．
∴直线PB的方程为：y=
x，联立
，解得yN=6．
直线PA的方程为：y=-
，∴yM=-
．
∴yN•yM=6×(-
)=-9．
②当直线AB的斜率存在时，设A（x1，y1），B（x2，y2）．则P（-x2，-y2）．
∴直线PB的方程为：y=
x，联立
，解得yN=
．
设直线AB的方程为：y=k（x-1）．
直线PA的方程为：kPA=
．
由
+
=1，
+
=1，
两式相减得
+
=0．
∴
+kPA•kAB=0，∴kPA=-
．
得到直线PA的方程为：y+y2=-
(x+x2)．
联立直线PA与l的方程
，
解得y=-y2-
=-
-y2=
．
∵
+
=1，∴4
+3
-12=0．
∴yM=-
．
∴yM•yN=-
•
=-9．
综上可知：yM•yN=-9，为定值．
∵过点(1，| 3 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
∴
|
∴椭圆C的标准方程为：
| x2 |
| 4 |
| y2 |
| 3 |
（2）∵点B的坐标为(
| 8 |
| 5 |
3
| ||
| 5 |
| 8 |
| 5 |
3
| ||
| 5 |
可得kBF=
| ||||
|
| 3 |
∴直线BF的方程y=
| 3 |
联立
|
| 8 |
| 5 |
把x=0代入直线方程可得y=-
| 3 |
∴A(0，-
| 3 |
∴kPA=
| ||||||
-
|
| ||
| 4 |
∴直线PA的方程为：y=-
| ||
| 4 |
| 3 |
（3）椭圆C的右准线l为：x=
| a2 |
| c |
①当直线AB⊥x轴时，B（1，
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴直线PB的方程为：y=
| 3 |
| 2 |
|
直线PA的方程为：y=-
| 3 |
| 2 |
| 3 |
| 2 |
∴yN•yM=6×(-
| 3 |
| 2 |
②当直线AB的斜率存在时，设A（x1，y1），B（x2，y2）．则P（-x2，-y2）．
∴直线PB的方程为：y=
| y2 |
| x2 |
|
| 4y2 |
| x2 |
设直线AB的方程为：y=k（x-1）．
直线PA的方程为：kPA=
| y1+y2 |
| x1+x2 |
由
| ||
| 4 |
| ||
| 3 |
| ||
| 4 |
| ||
| 3 |
两式相减得
| (x1+x2)(x1-x2) |
| 4 |
| (y1+y2)(y1-y2) |
| 3 |
∴
| 3 |
| 4 |
| 3 |
| 4k |
得到直线PA的方程为：y+y2=-
| 3 |
| 4k |
联立直线PA与l的方程
|
解得y=-y2-
| 3(4+x2) |
| 4k |
| 3(4+x2)(x2-1) |
| 4y2 |
-[4
| ||||
| 4y2 |
∵
| ||
| 4 |
| ||
| 3 |
| y | 2 2 |
| x | 2 2 |
∴yM=-
| 9x2 |
| 4y2 |
∴yM•yN=-
| 9x2 |
| 4y2 |
| 4y2 |
| x2 |
综上可知：yM•yN=-9，为定值．
点评：本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立、点与椭圆的位置关系、斜率计算公式直线的点斜式等基础知识与基本技能方法，考查了推理能力和计算能力，属于难题．
练习册系列答案
相关题目
如图，在平面直角坐标系xOy中，锐角α和钝角β的终边分别与单位圆交于A，B两点．若点A的横坐标是