题目内容
已知函数f(x)=2lnx-ax2,g(x)=x-
+
,a∈R,(e为自然对数的底数).
(1)讨论函数f(x)的极值;
(2)定义:若?x0∈R,使得f(x0)=x0成立,则称x0为函数y=f(x)的一个不动点.设h(x)=f(x)+g(x).当a>0时,讨论函数h(x)是否存在不动点,若存在求出a的范围,若不存在说明理由.
| e |
| a |
| 1 |
| 2 |
(1)讨论函数f(x)的极值;
(2)定义:若?x0∈R,使得f(x0)=x0成立,则称x0为函数y=f(x)的一个不动点.设h(x)=f(x)+g(x).当a>0时,讨论函数h(x)是否存在不动点,若存在求出a的范围,若不存在说明理由.
分析:(1)对f(x)求导,讨论f′(x)的值是大于0、还是小于0,从而确定f(x)在定义域上的极值情况;
(2)假设存在不动点,则方程h(x)=x有解,讨论方程的解是否存在,以确定h(x)有无不动点.
(2)假设存在不动点,则方程h(x)=x有解,讨论方程的解是否存在,以确定h(x)有无不动点.
解答:解:(1)∵f(x)=2lnx-ax2,∴f′(x)=
-2ax=
(其中x>0);
①当a=0时,f′(x)=
>0,∴f(x)在(0,+∞)上是增函数,无极值;
②当a<0时,f′(x)>0恒成立,∴f(x)在(0,+∞)上是增函数,无极值;
③当a>0时,令f′(x)=0,得x=
,列表如下:

∴当x=
时,f(x)有极大值是f(
)=-lna-1;
综上,当a≤0时无极值,当a>0时,f(x)有极大值是f(
)=-lna-1;
(2)假设存在不动点,则方程h(x)=x有解,即2lnx-ax2-
+
=0有解;
设r(x)=2lnx-ax2-
+
,(其中a>0),
由(1)知,r(x)极大值=-lna-1-
+
=-lna-
-
,
下面判断r(x)极大值是否大于0,设p(a)=-lna-
-
,(其中a>0),
∴p′(a)=-
+
=
,列表如下:
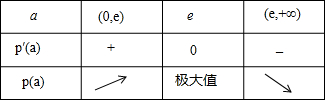
当a=e时,p(a)极大值=p(e)=-
<0,
所以,p(a)=-lna-
-
<0恒成立,即r(x)极大值小于零,
所以h(x)无不动点.
| 2 |
| x |
| 2-2ax2 |
| x |
①当a=0时,f′(x)=
| 2 |
| x |
②当a<0时,f′(x)>0恒成立,∴f(x)在(0,+∞)上是增函数,无极值;
③当a>0时,令f′(x)=0,得x=
|

∴当x=
|
|
综上,当a≤0时无极值,当a>0时,f(x)有极大值是f(
|
(2)假设存在不动点,则方程h(x)=x有解,即2lnx-ax2-
| e |
| a |
| 1 |
| 2 |
设r(x)=2lnx-ax2-
| e |
| a |
| 1 |
| 2 |
由(1)知,r(x)极大值=-lna-1-
| e |
| a |
| 1 |
| 2 |
| e |
| a |
| 1 |
| 2 |
下面判断r(x)极大值是否大于0,设p(a)=-lna-
| e |
| a |
| 1 |
| 2 |
∴p′(a)=-
| 1 |
| a |
| e |
| a2 |
| e-a |
| a2 |

当a=e时,p(a)极大值=p(e)=-
| 5 |
| 2 |
所以,p(a)=-lna-
| e |
| a |
| 1 |
| 2 |
所以h(x)无不动点.
点评:本题考查了利用导数来判定函数的单调性与极值问题,也考查了含参数的不等式的解法问题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目