题目内容
已知函数f（x）=1-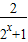
，（I）判断函数的奇偶性；
（Ⅱ）求函数f（x）的值域．
【答案】分析：（I）利用函数奇偶性的定义判断函数的奇偶性；
（Ⅱ）利用指数函数的性质确定函数的值域．
解答：解：（I）f（x）=1-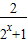
=
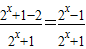，函数定义域为R，关于原点对称．
又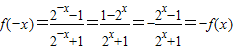
，所以函数f（x）是奇函数．
（Ⅱ）因为2x＞0，所以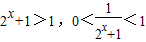
，
所以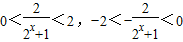
，
即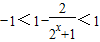
，所以-1＜y＜1．
故函数f（x）的值域为（-1，1）．
点评：本题主要考查函数奇偶性的应用以及函数值域的求法，要求熟练掌握函数的性质．
（Ⅱ）利用指数函数的性质确定函数的值域．
解答：解：（I）f（x）=1-
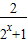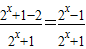=，函数定义域为R，关于原点对称．又
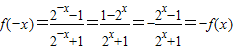，所以函数f（x）是奇函数．（Ⅱ）因为2x＞0，所以
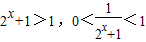，所以
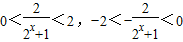，即
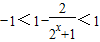，所以-1＜y＜1．故函数f（x）的值域为（-1，1）．
点评：本题主要考查函数奇偶性的应用以及函数值域的求法，要求熟练掌握函数的性质．
练习册系列答案
相关题目
已知函数f（x）=
，g（x）=1+
，若f（x）＞g（x），则实数x的取值范围是（ ）
| 1 |
| |x| |
| x+|x| |
| 2 |
| A、（-∞，-1）∪（0，1） | ||||
B、(-∞，-1)∪(0，
| ||||
C、(-1，0)∪(
| ||||
D、(-1，0)∪(0，
|