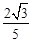题目内容
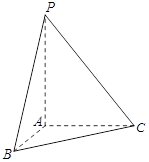
如图,已知点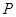 在圆柱
在圆柱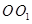 的底面圆
的底面圆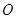 上,
上,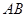 为圆
为圆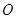 的直径,圆柱
的直径,圆柱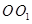 的表面积为
的表面积为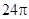 ,
,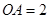 ,
,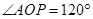 。
。
(1)求三棱锥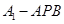 的体积。
的体积。
(2)求异面直线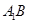 与
与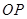 所成角的余弦值;
所成角的余弦值;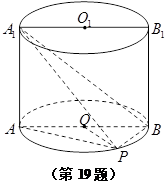
 在圆柱
在圆柱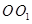 的底面圆
的底面圆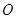 上,
上,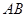 为圆
为圆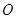 的直径,圆柱
的直径,圆柱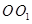 的表面积为
的表面积为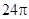 ,
,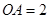 ,
,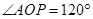 。
。(1)求三棱锥
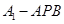 的体积。
的体积。(2)求异面直线
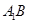 与
与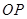 所成角的余弦值;
所成角的余弦值;
(1)
 ;(2)
;(2)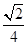 .
.

 ;(2)
;(2)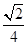 .
. 本试题主要是考查了棱锥的体积和异面直线的所成角的余弦值的求解的综合运用。
(1)因为根据已知条件中圆柱的表面积和长度和角度问题可知得到锥体的底面的面积的求解以及最终的体积的表示。
(2)因为异面直线的所成的角一般通过平移得到,那么平移后的夹角为所求的异面直线的角。
解:
(1)由题意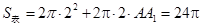 ,解得
,解得 . -------------------2分
. -------------------2分
在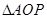 中,
中,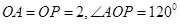 ,所以
,所以 -------------------3分
-------------------3分
在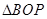 中,
中,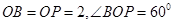 ,所以
,所以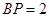 -------------------4分
-------------------4分
 -------------------5分
-------------------5分
 -------------------6分
-------------------6分
(2)取 中点
中点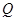 ,连接
,连接 ,
,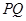 ,则
,则 ,
,
得 或它的补角为异面直线
或它的补角为异面直线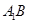 与
与 所成的角. -------------------8分
所成的角. -------------------8分
又 ,
, ,得
,得 ,
,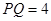 , -------------------10分
, -------------------10分
由余弦定理得 ,
,
所以异面直线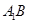 与
与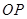 所成角的余弦值是
所成角的余弦值是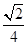 .-------------------12分
.-------------------12分
(1)因为根据已知条件中圆柱的表面积和长度和角度问题可知得到锥体的底面的面积的求解以及最终的体积的表示。
(2)因为异面直线的所成的角一般通过平移得到,那么平移后的夹角为所求的异面直线的角。
解:
(1)由题意
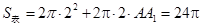 ,解得
,解得 . -------------------2分
. -------------------2分 在
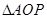 中,
中,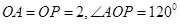 ,所以
,所以 -------------------3分
-------------------3分在
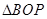 中,
中,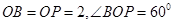 ,所以
,所以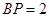 -------------------4分
-------------------4分 -------------------5分
-------------------5分 -------------------6分
-------------------6分(2)取
 中点
中点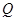 ,连接
,连接 ,
,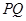 ,则
,则 ,
,得
 或它的补角为异面直线
或它的补角为异面直线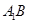 与
与 所成的角. -------------------8分
所成的角. -------------------8分 又
 ,
, ,得
,得 ,
,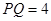 , -------------------10分
, -------------------10分 由余弦定理得
 ,
,所以异面直线
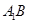 与
与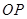 所成角的余弦值是
所成角的余弦值是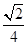 .-------------------12分
.-------------------12分
练习册系列答案
相关题目
 中,
中, ,
, ,点
,点 ,
, 分别是
分别是 ,
, 的中点.
的中点.
 ⊥平面
⊥平面 ;
; ⊥平面
⊥平面 ,求三棱锥
,求三棱锥 的体积.
的体积. 中,底面
中,底面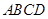 为正方形,
为正方形,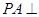 平面
平面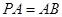 ,点
,点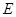 是
是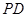 的中点.
的中点.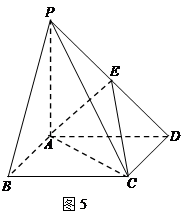
 //平面
//平面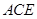 ;
;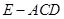 的体积为
的体积为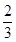 ,求
,求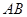 的长.
的长.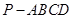 的底面是边长为1的正方形,
的底面是边长为1的正方形,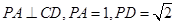
 平面
平面
 ,且
,且 ,以BD为折线,把
,以BD为折线,把 折起,使平面
折起,使平面 ,连AC。
,连AC。
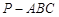 ,
,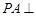 平面
平面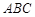 ,
,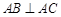 ,
,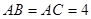 ,
,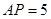 .
.
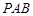 (及其内部)绕
(及其内部)绕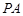 所在直线旋转一周形成一几何体,求该几何体的体积
所在直线旋转一周形成一几何体,求该几何体的体积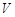 ;
; 的余弦值.
的余弦值.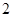 ,一侧棱到对面的距离不小于
,一侧棱到对面的距离不小于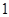 ,从此三棱柱中去掉以此侧棱为直径的球所占的部分,余下的几何体的表面积与原三棱柱的表面积相等,则所剩几何体的体积最小值为 .
,从此三棱柱中去掉以此侧棱为直径的球所占的部分,余下的几何体的表面积与原三棱柱的表面积相等,则所剩几何体的体积最小值为 . 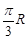 ,则北纬45°圈所在平面与过A、B两点的球的大圆面所成的二面角的余弦值为 ( )
,则北纬45°圈所在平面与过A、B两点的球的大圆面所成的二面角的余弦值为 ( ) 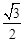 (B)
(B)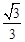 (C)
(C)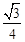 (D)
(D)