题目内容
在极坐标系中,点 到圆ρ=2cosθ的圆心的距离是 .
到圆ρ=2cosθ的圆心的距离是 .
【答案】分析:先将极坐标方程化为一般方程,然后再计算点 到圆ρ=2cosθ的圆心的距离.
到圆ρ=2cosθ的圆心的距离.
解答:解:∵在极坐标系中,ρ=2cosθ,∴x=pcosθ,y=psinθ,消去p和θ得,
∴(x-1)2+y2=1,
∴圆心的直角坐标是(1,0),半径长为1.
∴点 在一般方程坐标为(1,
在一般方程坐标为(1, ),
),
∴点 到圆ρ=2cosθ的圆心的距离是 d=
到圆ρ=2cosθ的圆心的距离是 d= =
= ,
,
故答案为 .
.
点评:此题考查极坐标方程与普通方程的区别和联系,两者要会互相转化,根据实际情况选择不同的方程进行求解,这也是每年高考必考的热点问题.
 到圆ρ=2cosθ的圆心的距离.
到圆ρ=2cosθ的圆心的距离.解答:解:∵在极坐标系中,ρ=2cosθ,∴x=pcosθ,y=psinθ,消去p和θ得,
∴(x-1)2+y2=1,
∴圆心的直角坐标是(1,0),半径长为1.
∴点
 在一般方程坐标为(1,
在一般方程坐标为(1, ),
),∴点
 到圆ρ=2cosθ的圆心的距离是 d=
到圆ρ=2cosθ的圆心的距离是 d= =
= ,
,故答案为
 .
.点评:此题考查极坐标方程与普通方程的区别和联系,两者要会互相转化,根据实际情况选择不同的方程进行求解,这也是每年高考必考的热点问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在极坐标系中,点 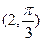 到圆
到圆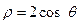 的圆心的距离为
的圆心的距离为
| A.2 | B. | C. | D.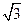 |
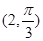 到圆
到圆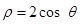 的圆心的距离为(
).
的圆心的距离为(
).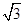 C.
C.
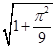 D
D
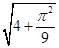
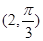 到圆
到圆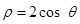 的圆心的距离为( )
的圆心的距离为( )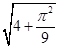 C.
C.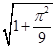 D.
D.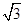
 到圆ρ=2cosθ的圆心的距离为
到圆ρ=2cosθ的圆心的距离为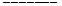
 到圆
到圆 的圆心的距离为
的圆心的距离为 (C)
(C)
 (D)
(D) 