题目内容
16.若实数x、y满足sinx-$\sqrt{3}$cosx≤y≤0,-$\frac{2π}{3}$≤x≤$\frac{π}{3}$,则目标函数z=x+y的最小值是( )| A. | -$\frac{2π}{3}$ | B. | -2 | C. | $-\frac{{3\sqrt{3}}}{2}$ | D. | -$\frac{π}{3}$-$\sqrt{3}$ |
分析 作出不等式组对应的平面区域,利用目标函数的几何意义进行求解.
解答 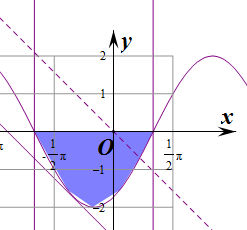 解:作出不等式组对应的平面区域如图:(阴影部分).
解:作出不等式组对应的平面区域如图:(阴影部分).
由z=x+y得y=-x+z,平移直线y=-x+z,
由图象可知当直线y=-x+z和曲线y=sinx-$\sqrt{3}$cosx相切时,
直线y=-x+z的截距最小,此时z最小.
由f′(x)=cosx+$\sqrt{3}$sinx=-1,
即2sin(x+$\frac{π}{6}$)=-1,
即sin(x+$\frac{π}{6}$)=-$\frac{1}{2}$,
∵-$\frac{2π}{3}$≤x≤$\frac{π}{3}$,
∴-$\frac{π}{2}$≤x+$\frac{π}{6}$≤$\frac{π}{2}$,
即x+$\frac{π}{6}$=-$\frac{π}{6}$,
x=-$\frac{π}{3}$,
此时y=sin(-$\frac{π}{3}$)-$\sqrt{3}×$cos(-$\frac{π}{3}$)=-$\frac{\sqrt{3}}{2}$-$\frac{\sqrt{3}}{2}$=-$\sqrt{3}$,
即切点坐标为(-$\frac{π}{3}$,$-\sqrt{3}$),
代入目标函数得z=-$\frac{π}{3}$-$\sqrt{3}$.
故选:D.
点评 本题主要考查线性规划的应用,根据三角函数的图象,结合直线和曲线的相切问题是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.若函数f(x)=$\root{3}{x}$•$\sqrt{x}$,则f′(x)=( )
| A. | $\frac{5}{6}$x | B. | $\frac{5}{6}$$\root{6}{x}$ | C. | $\frac{5}{6\root{6}{x}}$ | D. | $\frac{6}{5}$$\root{6}{x}$ |
4.等比数列{an}满足a2+8a5=0,设数列{$\frac{1}{{a}_{n}}$}的前n项和为Sn,则$\frac{{S}_{5}}{{S}_{2}}$=( )
| A. | -11 | B. | -8 | C. | 5 | D. | 11 |
1.已知等比数列{an}的公比q=2,前n项和为Sn,若S4=1,则S8=( )
| A. | 15 | B. | 17 | C. | 19 | D. | 21 |
8.函数y=sinxsin($\frac{π}{2}$-x)的最小正周期是( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |