题目内容
下列命题中,真命题是( )
A.?x∈R,sin2
| ||||||
| B.?x∈(0,π),sinx>cosx | ||||||
| C.?x∈R,x2+x=-1 | ||||||
| D.?x∈(0,+∞),ex>1+x |
对于A,由同角三角函数和平方关系,我们知道?x∈R,sin2
+cos2
=1,所以A为假命题;
对于B,取特殊值:当时x=
时,sinx=cosx=
,所以B为假命题;
对于C,一元二次方程根的判别式△=1-4=-3<0,所以原方程没有实数根,所以C为假命题;
对于D,构造函数y=ex-x,x∈(0,+∞)
求出导数:y/=ex-1,可得当时y/<0,函数为减函数,
当x∈(1,+∞)时y/>0,函数为增函数,
所以当x=1时函数的最小值为e-1,即?x∈(0,+∞),ex-x≥e-1>1,
移项,得ex>1+x,因此“?x∈(0,+∞),ex>1+x”是真命题
故选D
| x |
| 2 |
| x |
| 2 |
对于B,取特殊值:当时x=
| π |
| 4 |
| ||
| 2 |
对于C,一元二次方程根的判别式△=1-4=-3<0,所以原方程没有实数根,所以C为假命题;
对于D,构造函数y=ex-x,x∈(0,+∞)
求出导数:y/=ex-1,可得当时y/<0,函数为减函数,
当x∈(1,+∞)时y/>0,函数为增函数,
所以当x=1时函数的最小值为e-1,即?x∈(0,+∞),ex-x≥e-1>1,
移项,得ex>1+x,因此“?x∈(0,+∞),ex>1+x”是真命题
故选D

练习册系列答案
相关题目
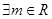 ,使函数
,使函数 是偶函数
是偶函数 ,使函数
,使函数 ≤0
≤0 =-1
=-1