题目内容
已知函数f(x)=lnx, .
.
(Ⅰ)设函数F(x)=f(x)-ag(x),若x∈(0,2),函数F(x)不存在极值,求实数a的取值范围;
(Ⅱ)设函数 ,如果对于任意实数x∈(1,t],都有不等式tG(x)-xG(t)≤G(x)-G(t)成立,求实数t的最大值.
,如果对于任意实数x∈(1,t],都有不等式tG(x)-xG(t)≤G(x)-G(t)成立,求实数t的最大值.
解:(I)由 ,得
,得 ,
,
当a≤0时,F'(x)>0(x>0),此时F(x)在(0,2)上无极值,
当a>0时,所以F(x)在区间 上递增,在区间
上递增,在区间 上递减,
上递减,
所以要使得F(x)在(0,2)上不存在极值,只要 ,即
,即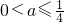 ,
,
综合以上两种情况可得 .(6分)
.(6分)
(II)不等式tG(x)-xG(t)≤G(x)-G(t)等价于(t-1)G(x)≤(x-1)G(t),
等价于 ,即
,即 …(8分)
…(8分)
设函数 ,问题等价于h(x)≤h(t)在(1,t]上恒成立,
,问题等价于h(x)≤h(t)在(1,t]上恒成立,
即h(t)为h(x)的最大值,而 ,所以
,所以 ,(12分)
,(12分)
故h(x)在区间(e,+∞)上单调递减,在区间(1,e)上单调递增,
因此t≤e,即实数t的最大值为e. (14分)
分析:(Ⅰ)求导数可得 ,分当a≤0,和a>0两种情形来考虑,综合可得a的范围;
,分当a≤0,和a>0两种情形来考虑,综合可得a的范围;
(Ⅱ)经过多次等价转化,问题等价于 ,设函数
,设函数 ,问题等价于h(x)≤h(t)在(1,t]上恒成立,求导数可得h(x)的单调性,进而可得最值,可得结论.
,问题等价于h(x)≤h(t)在(1,t]上恒成立,求导数可得h(x)的单调性,进而可得最值,可得结论.
点评:本题考查导数法研究函数的单调性和极值问题,涉及等价转化法,属中档题.
 ,得
,得 ,
,当a≤0时,F'(x)>0(x>0),此时F(x)在(0,2)上无极值,
当a>0时,所以F(x)在区间
 上递增,在区间
上递增,在区间 上递减,
上递减,所以要使得F(x)在(0,2)上不存在极值,只要
 ,即
,即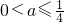 ,
,综合以上两种情况可得
 .(6分)
.(6分)(II)不等式tG(x)-xG(t)≤G(x)-G(t)等价于(t-1)G(x)≤(x-1)G(t),
等价于
 ,即
,即 …(8分)
…(8分)设函数
 ,问题等价于h(x)≤h(t)在(1,t]上恒成立,
,问题等价于h(x)≤h(t)在(1,t]上恒成立,即h(t)为h(x)的最大值,而
 ,所以
,所以 ,(12分)
,(12分)故h(x)在区间(e,+∞)上单调递减,在区间(1,e)上单调递增,
因此t≤e,即实数t的最大值为e. (14分)
分析:(Ⅰ)求导数可得
 ,分当a≤0,和a>0两种情形来考虑,综合可得a的范围;
,分当a≤0,和a>0两种情形来考虑,综合可得a的范围;(Ⅱ)经过多次等价转化,问题等价于
 ,设函数
,设函数 ,问题等价于h(x)≤h(t)在(1,t]上恒成立,求导数可得h(x)的单调性,进而可得最值,可得结论.
,问题等价于h(x)≤h(t)在(1,t]上恒成立,求导数可得h(x)的单调性,进而可得最值,可得结论.点评:本题考查导数法研究函数的单调性和极值问题,涉及等价转化法,属中档题.

练习册系列答案
相关题目