题目内容
某公司决定采用增加广告投入和技术改造投入两项措施来获得更大的收益.通过对市场的预测,当对两项投入都不大于3(百万元)时,每投入x(百万元)广告费,增加的销售额可近似的用函数y1=-2x2+14x(百万元)来计算;每投入x(百万元)技术改造费用,增加的销售额可近似的用函数y2=- x3+2x2+5x(百万元)来计算.现该公司准备共投入3(百万元),分别用于广告投入和技术改造投入,请设计一种资金分配方案,使得该公司的销售额最大. (参考数据:
x3+2x2+5x(百万元)来计算.现该公司准备共投入3(百万元),分别用于广告投入和技术改造投入,请设计一种资金分配方案,使得该公司的销售额最大. (参考数据: ≈1.41,
≈1.41, ≈1.73)
≈1.73)
解:设3百万元中技术改造投入为x(百万元),广告费投入为3-x(百万元),则广告收入带来的销售额增加值为-2(3-x)2+14(3-x)(百万元),技术改造投入带来的销售额增加值为- x3+2x2+5x(百万元),
x3+2x2+5x(百万元),
所以,投入带来的销售额增加值F(x)=-2(3-x)2+14(3-x)- x3+2x2+5x.
x3+2x2+5x.
整理上式得F(x)=- x3+3x+24,
x3+3x+24,
因为F′(x)=-x2+3,令F′(x)=0,解得x= 或x=-
或x=- (舍去),
(舍去),
当x∈[0, ),F′(x)>0,当x∈(
),F′(x)>0,当x∈( ,3]时,F′(x)<0,
,3]时,F′(x)<0,
所以,x= ≈1.73时,F(x)取得最大值.
≈1.73时,F(x)取得最大值.
所以,当该公司用于广告投入1.27(百万元),用于技术改造投入1.73(百万元)时,公司将有最大的销售额.
分析:先计算投入带来的销售额增加值,再利用导数法,即可确定函数的最值.
点评:本题考查函数模型的构建,考查导数知识的运用,考查学生的计算能力,正确确定函数解析式是关键.
 x3+2x2+5x(百万元),
x3+2x2+5x(百万元),所以,投入带来的销售额增加值F(x)=-2(3-x)2+14(3-x)-
 x3+2x2+5x.
x3+2x2+5x.整理上式得F(x)=-
 x3+3x+24,
x3+3x+24,因为F′(x)=-x2+3,令F′(x)=0,解得x=
 或x=-
或x=- (舍去),
(舍去),当x∈[0,
 ),F′(x)>0,当x∈(
),F′(x)>0,当x∈( ,3]时,F′(x)<0,
,3]时,F′(x)<0,所以,x=
 ≈1.73时,F(x)取得最大值.
≈1.73时,F(x)取得最大值.所以,当该公司用于广告投入1.27(百万元),用于技术改造投入1.73(百万元)时,公司将有最大的销售额.
分析:先计算投入带来的销售额增加值,再利用导数法,即可确定函数的最值.
点评:本题考查函数模型的构建,考查导数知识的运用,考查学生的计算能力,正确确定函数解析式是关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
某公司决定给员工增加工资,提出了两个方案,让每位员工自由选择其中一种.甲方案是:公司在每年年末给每位员工增资1000元;乙方案是每半年末给每位员工增资300元.某员工分别依两种方案计算增资总额后得到下表:
| 工作年限 | 方案甲 | 方案乙 | 最终选择 |
| 1 | 1000 | 600 | 方案甲 |
| 2 | 2000 | 1200 | 方案乙 |
| ≥3 | 方案甲 |
(说明:①方案的选择应以让自己获得更多增资为准. ②假定员工工作年限均为整数.)
(1)他这样计算增资总额,结果对吗?如果让你选择,你会怎样选择增资方案?说明你的理由;
(2)若保持方案甲不变,而方案乙中每半年末的增资数改为a元,问:a为何值时,方案乙总比方案甲多增资?
(8分) 抛掷骰子,是大家非常熟悉的日常游戏了.
某公司决定以此玩抛掷(两颗)骰子的游戏,来搞一个大型的促销活动——“轻轻松松抛骰子,欢欢乐乐拿礼券”.
方案1:总点数是几就送礼券几十元.
|
总点数 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
礼券额 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
方案2:总点数为中间数7时的礼券最多,为120元;以此为基准,总点数每减少或增加1,礼券减少20元.
|
总点数 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
礼券额 |
20 |
40 |
60 |
80 |
100 |
120 |
100 |
80 |
60 |
40 |
20 |
方案3 总点数为2和12时的礼券最多,都为120元;点数从2到7递增或从12到7递减时,礼券都依次减少20元.
|
总点数 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
礼券额 |
120 |
100 |
80 |
60 |
40 |
20 |
40 |
60 |
80 |
100 |
120 |
如果你是该公司老总,你准备怎样去选择促销方案?请你对以上三种方案给出裁决.
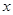 (百万元)广告费,增加的销售额可近似的用函数
(百万元)广告费,增加的销售额可近似的用函数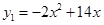 (百万元)来计算;每投入x(百万元)技术改造费用,增加的销售额可近似的用函数
(百万元)来计算;每投入x(百万元)技术改造费用,增加的销售额可近似的用函数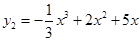 (百万元)来计算.现该公司准备共投入3(百万元),分别用于广告投入和技术改造投入,请设计一种资金分配方案,使得该公司的销售额最大. (参考数据:≈1.41,≈1.73)
(百万元)来计算.现该公司准备共投入3(百万元),分别用于广告投入和技术改造投入,请设计一种资金分配方案,使得该公司的销售额最大. (参考数据:≈1.41,≈1.73)