题目内容
[1]已知矩阵 ,若矩阵A属于特征值6的一个特征向量为
,若矩阵A属于特征值6的一个特征向量为 ,属于特征值1的一个特征向量为
,属于特征值1的一个特征向量为 .
.(1)求矩阵A,并写出A的逆矩阵;
(2)若向量
 ,试计算M50β.
,试计算M50β.[2]已知
 是定义在区间[-1,1]上的函数,设x1,x2∈[-1,1]且x1≠x2.
是定义在区间[-1,1]上的函数,设x1,x2∈[-1,1]且x1≠x2.(1)求证:|f(x1)-f(x2)|≤|x1-x2|;
(2)若a2+b2=1,求证:
 .
.
【答案】分析:[1](1)由矩阵A属于特征值6的一个特征向量为α1= 可得,c+d=6;由矩阵A属于特征值1的一个特征向量为α2=
可得,c+d=6;由矩阵A属于特征值1的一个特征向量为α2= ,
,
可得3c-2d=-2,由此能求出矩阵A和A的逆矩阵.
(2)令β=mα1+nα2可解得m=5,n=-1,即β=5α1-α2.由此能求出M50β.
[2](1)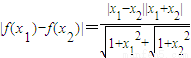 ,由此可证明|f(x1)-f(x2)|≤|x1-x2|;
,由此可证明|f(x1)-f(x2)|≤|x1-x2|;
(2)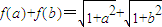 由此能够推导出
由此能够推导出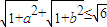 .
.
解答:解:[1](1)由矩阵A属于特征值6的一个特征向量为α1= 可得,
可得,

 =6
=6 ,即c+d=6;(1分)
,即c+d=6;(1分)
由矩阵A属于特征值1的一个特征向量为α2= ,
,
可得
 =
= ,即3c-2d=-2,(2分)
,即3c-2d=-2,(2分)
解得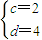 即A=
即A= ,(3分)
,(3分)
A逆矩阵是 .(5分)
.(5分)
(2)令β=mα1+nα2可解得m=5,n=-1,即β=5α1-α2.(7分)
所以M50β=M50(5α1-α2)
=5(M50α1)-(M50α2)
=5(λ150α1)-(λ250α2)
=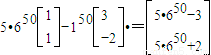 .(10分)
.(10分)
(选修4-5:不等式选讲)
证:[2](1)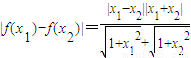
∵|x1+x2|≤|x1|+|x2|,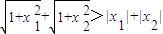 ,
,
∴|f(x1)-f(x2)|<|x1-x2|.(5分)
(2)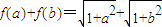 ,
,
∵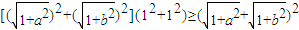 a2+b2=1,
a2+b2=1,
∴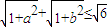 .(10分)
.(10分)
点评:本题考查二阶行列式的性质和应用,解题时要认真审题,仔细求解,注意公式的灵活运用.
 可得,c+d=6;由矩阵A属于特征值1的一个特征向量为α2=
可得,c+d=6;由矩阵A属于特征值1的一个特征向量为α2= ,
,可得3c-2d=-2,由此能求出矩阵A和A的逆矩阵.
(2)令β=mα1+nα2可解得m=5,n=-1,即β=5α1-α2.由此能求出M50β.
[2](1)
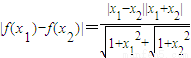 ,由此可证明|f(x1)-f(x2)|≤|x1-x2|;
,由此可证明|f(x1)-f(x2)|≤|x1-x2|;(2)
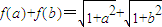 由此能够推导出
由此能够推导出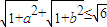 .
.解答:解:[1](1)由矩阵A属于特征值6的一个特征向量为α1=
 可得,
可得,
 =6
=6 ,即c+d=6;(1分)
,即c+d=6;(1分)由矩阵A属于特征值1的一个特征向量为α2=
 ,
,可得

 =
= ,即3c-2d=-2,(2分)
,即3c-2d=-2,(2分)解得
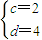 即A=
即A= ,(3分)
,(3分)A逆矩阵是
 .(5分)
.(5分)(2)令β=mα1+nα2可解得m=5,n=-1,即β=5α1-α2.(7分)
所以M50β=M50(5α1-α2)
=5(M50α1)-(M50α2)
=5(λ150α1)-(λ250α2)
=
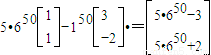 .(10分)
.(10分)(选修4-5:不等式选讲)
证:[2](1)
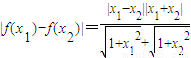
∵|x1+x2|≤|x1|+|x2|,
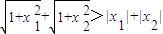 ,
,∴|f(x1)-f(x2)|<|x1-x2|.(5分)
(2)
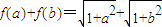 ,
,∵
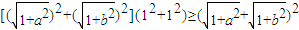 a2+b2=1,
a2+b2=1,∴
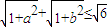 .(10分)
.(10分)点评:本题考查二阶行列式的性质和应用,解题时要认真审题,仔细求解,注意公式的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA, ,PD=1,BD=8,求线段BC的长.
,PD=1,BD=8,求线段BC的长. ,矩阵阵
,矩阵阵 ,
, ,求在矩阵
,求在矩阵 作用下变换所得到的图形的面积.
作用下变换所得到的图形的面积. (
( 为参数,
为参数, 为常数且
为常数且 )被以原点为极点,
)被以原点为极点, 轴的正半轴为极轴,方程为
轴的正半轴为极轴,方程为 的曲线所截,求截得的弦长.
的曲线所截,求截得的弦长. ,求证:
,求证: .
.