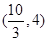题目内容
已知抛物线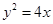 和点
和点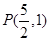 ,过点P的直线
,过点P的直线 与抛物线交与
与抛物线交与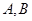 两点,设点P刚好为弦
两点,设点P刚好为弦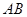 的中点。
的中点。
(1)求直线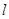 的方程
的方程
(2)若过线段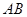 上任一
上任一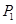 (不含端点
(不含端点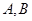 )作倾斜角为
)作倾斜角为 的直线
的直线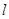 交抛物线于
交抛物线于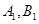 ,类比圆中的相交弦定理,给出你的猜想,若成立,给出证明;若不成立,请说明理由。
,类比圆中的相交弦定理,给出你的猜想,若成立,给出证明;若不成立,请说明理由。
(3)过P作斜率分别为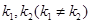 的直线
的直线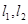 ,
,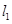 交抛物线于
交抛物线于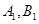 ,
,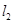 交抛物线于
交抛物线于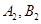 ,是否存在
,是否存在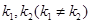 使得(2)中的猜想成立,若存在,给出
使得(2)中的猜想成立,若存在,给出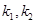 满足的条件。若不存在,请说明理由。
满足的条件。若不存在,请说明理由。
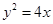 和点
和点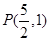 ,过点P的直线
,过点P的直线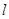 与抛物线交与
与抛物线交与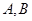 两点,设点P刚好为弦
两点,设点P刚好为弦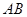 的中点。
的中点。(1)求直线
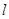 的方程
的方程(2)若过线段
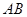 上任一
上任一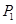 (不含端点
(不含端点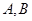 )作倾斜角为
)作倾斜角为 的直线
的直线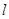 交抛物线于
交抛物线于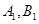 ,类比圆中的相交弦定理,给出你的猜想,若成立,给出证明;若不成立,请说明理由。
,类比圆中的相交弦定理,给出你的猜想,若成立,给出证明;若不成立,请说明理由。(3)过P作斜率分别为
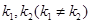 的直线
的直线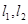 ,
,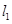 交抛物线于
交抛物线于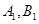 ,
,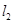 交抛物线于
交抛物线于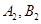 ,是否存在
,是否存在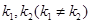 使得(2)中的猜想成立,若存在,给出
使得(2)中的猜想成立,若存在,给出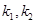 满足的条件。若不存在,请说明理由。
满足的条件。若不存在,请说明理由。(1)

(2)猜想



(2)猜想



略

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 为焦点的抛物线
为焦点的抛物线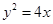 上的两点
上的两点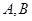 满足
满足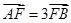 ,则弦
,则弦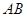 的中点到准线的距离为( )
的中点到准线的距离为( )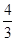
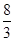
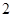
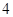
 与双曲线
与双曲线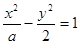 有相同的焦点,则
有相同的焦点,则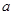 的值是
的值是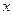 轴上,短轴长为4,离心率为
轴上,短轴长为4,离心率为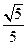 .
. 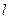 过该椭圆的左焦点,交椭圆于M、N两点,且
过该椭圆的左焦点,交椭圆于M、N两点,且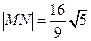 ,求直线
,求直线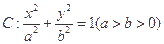 的离心率为
的离心率为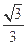 ,过右焦点F的直线
,过右焦点F的直线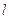 与
与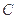 相交于
相交于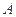 、
、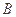 两点,当
两点,当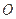 到
到
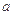 ,
,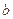 的值;
的值;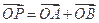 成立?
成立?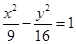 有共同渐近线,且过点(-3,
有共同渐近线,且过点(-3,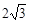 )的双曲线方程;
)的双曲线方程;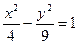 的渐近线方程是 (用一般式表示)
的渐近线方程是 (用一般式表示)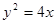 及椭圆
及椭圆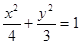 的实线上运动,若
的实线上运动,若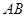 ∥
∥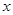 轴,点N的坐标
轴,点N的坐标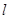 的取值范围是 ( )
的取值范围是 ( )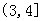 B.
B.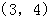 C.
C.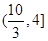 D.
D.