题目内容
已知a∈R,函数f(x)=xln(-x)+(a-1)x,(注:[ln(-x)] ′= )
)
(Ⅰ)若f(x)在x=-e处取得极值,求函数f(x)的单调区间;
(Ⅱ)求函数f(x)在区间[-e2,-e-1]上的最大值g(a)。
 )
)(Ⅰ)若f(x)在x=-e处取得极值,求函数f(x)的单调区间;
(Ⅱ)求函数f(x)在区间[-e2,-e-1]上的最大值g(a)。
解:(Ⅰ)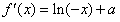 ,
,
由题意知x=-e时, ,即:
,即: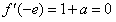 , ∴a=-1,
, ∴a=-1,
∴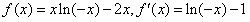 ,
,
令 ,可得x=-e;
,可得x=-e;
令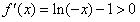 ,可得x<-e;
,可得x<-e;
令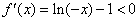 ,可得-e<x<0;
,可得-e<x<0;
∴f(x)在(-∞,-e)上是增函数,在(-e,0)上是减函数。
(Ⅱ)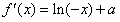 ,
,
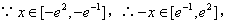
∴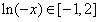 ,
,
①若a≥1,则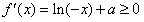 恒成立,此时f(x)在
恒成立,此时f(x)在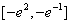 上是增函数,
上是增函数,
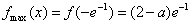 ;
;
②若a≤-2,则 恒成立,此时f(x)在
恒成立,此时f(x)在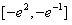 上是减函数,
上是减函数,
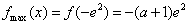 ;
;
③若-2<a<1,则令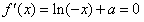 ,可得
,可得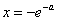 ,
,
∵ 是减函数,
是减函数,
∴当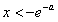 时,
时,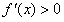 ;当
;当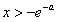 时,
时,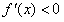 ,
,
∴f(x)在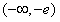
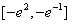 上左增右减,
上左增右减,
∴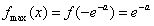 ;
;
综上: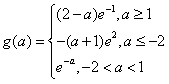 。
。
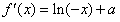 ,
,由题意知x=-e时,
 ,即:
,即: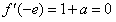 , ∴a=-1,
, ∴a=-1,∴
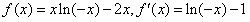 ,
,令
 ,可得x=-e;
,可得x=-e;令
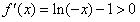 ,可得x<-e;
,可得x<-e;令
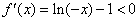 ,可得-e<x<0;
,可得-e<x<0;∴f(x)在(-∞,-e)上是增函数,在(-e,0)上是减函数。
(Ⅱ)
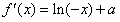 ,
,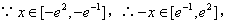
∴
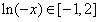 ,
,①若a≥1,则
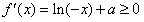 恒成立,此时f(x)在
恒成立,此时f(x)在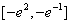 上是增函数,
上是增函数,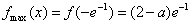 ;
;②若a≤-2,则
 恒成立,此时f(x)在
恒成立,此时f(x)在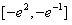 上是减函数,
上是减函数,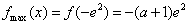 ;
;③若-2<a<1,则令
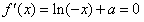 ,可得
,可得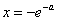 ,
,∵
 是减函数,
是减函数,∴当
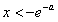 时,
时,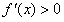 ;当
;当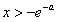 时,
时,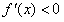 ,
,∴f(x)在
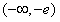
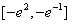 上左增右减,
上左增右减,∴
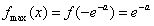 ;
;综上:
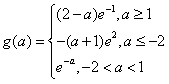 。
。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目