题目内容
已知数列{an}是首项为1,公差为d的等差数列,数列{bn}是首项为1,公比为q(q>1)的等比数列.
(1)若a5=b5,q=3,求数列{an•bn}的前n项和;
(2)若存在正整数k(k≥2),使得ak=bk.试比较an与bn的大小,并说明理由.
解:(1)依题意, ,
,
故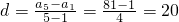 ,
,
所以an=1+20(n-1)=20n-19,
令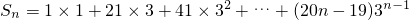 ,①
,①
则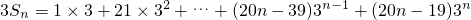 ,②
,②
①-②得,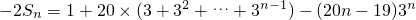 =
=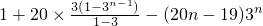 =(29-20n)•3n-29,
=(29-20n)•3n-29,
所以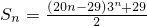 .
.
(2)因为ak=bk,所以1+(k-1)d=qk-1,即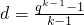 ,
,
故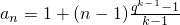 ,
,
又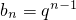 ,
,
所以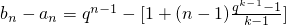
=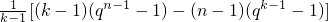
=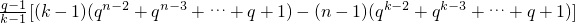 ,
,
(ⅰ)当1<n<k时,由q>1知,

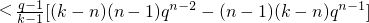
=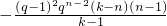 <0;
<0;
(ⅱ)当n>k时,由q>1知,
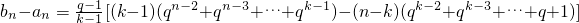
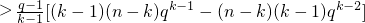
=(q-1)2qk-2(n-k)>0,
综上所述,当1<n<k时,an>bn;当n>k时,an<bn;当n=1时,an=bn.
分析:(1)由q=3,b1=1可求得b5,从而得到a5,由a1=1及通项公式可求得an,利用错位相减法即可求得数列{an•bn}的前n项和;
(2)由ak=bk,即1+(k-1)d=qk-1,得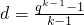 ,
,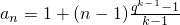 ,作差bn-an变形,然后分1<n<k时,当n>k时,n=1三种情况讨论讨论差的符号即可作出大小比较;
,作差bn-an变形,然后分1<n<k时,当n>k时,n=1三种情况讨论讨论差的符号即可作出大小比较;
点评:本题考查等差数列、等比数列的综合、数列求和,考查分类讨论思想,考查学生分析问题解决问题的能力,本题综合性强,难度较大.
 ,
,故
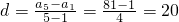 ,
,所以an=1+20(n-1)=20n-19,
令
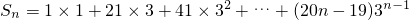 ,①
,①则
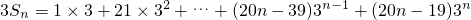 ,②
,②①-②得,
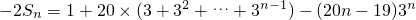 =
=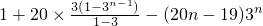 =(29-20n)•3n-29,
=(29-20n)•3n-29,所以
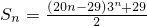 .
. (2)因为ak=bk,所以1+(k-1)d=qk-1,即
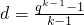 ,
,故
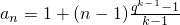 ,
,又
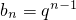 ,
,所以
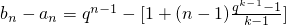
=
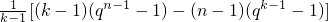
=
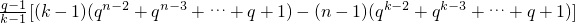 ,
,(ⅰ)当1<n<k时,由q>1知,

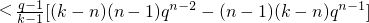
=
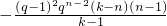 <0;
<0;(ⅱ)当n>k时,由q>1知,
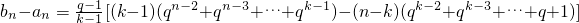
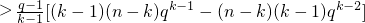
=(q-1)2qk-2(n-k)>0,
综上所述,当1<n<k时,an>bn;当n>k时,an<bn;当n=1时,an=bn.
分析:(1)由q=3,b1=1可求得b5,从而得到a5,由a1=1及通项公式可求得an,利用错位相减法即可求得数列{an•bn}的前n项和;
(2)由ak=bk,即1+(k-1)d=qk-1,得
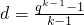 ,
,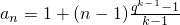 ,作差bn-an变形,然后分1<n<k时,当n>k时,n=1三种情况讨论讨论差的符号即可作出大小比较;
,作差bn-an变形,然后分1<n<k时,当n>k时,n=1三种情况讨论讨论差的符号即可作出大小比较;点评:本题考查等差数列、等比数列的综合、数列求和,考查分类讨论思想,考查学生分析问题解决问题的能力,本题综合性强,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目