题目内容
如图,正方形ABCD中,P是对角线BD上的一点,PECF是矩形,用向量证明PA=EF.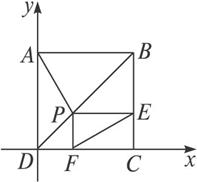
思路分析:用向量的坐标法证明,只要写出PA与EF的坐标,利用两点间距离公式就可得证.问题的关键在于如何建立坐标系,考虑到四边形ABCD,故可以D点为坐标原点,以DC、AD边所在直线分别为x、y轴,建立坐标系.

证明:建立如图所示的坐标系,设正方形的边长为a,|![]() |=λ(λ>0),
|=λ(λ>0),
则A(0,a),P(![]() λ,
λ,![]() λ),E(a,
λ),E(a,![]() λ),F(
λ),F(![]() λ,0),
λ,0),
∴![]() =(
=(![]() λ,a-
λ,a-![]() λ),
λ),![]() =(
=(![]() λ-a,
λ-a,![]() λ).
λ).
∵|![]() |2=λ2-
|2=λ2-![]() aλ+a2,|
aλ+a2,|![]() |2=λ2-
|2=λ2-![]() aλ+a2,
aλ+a2,
∴|![]() |2=|
|2=|![]() |2,故PA=EF.
|2,故PA=EF.

练习册系列答案
相关题目
 如图正方形ABCD,ABEF的边长都是1,而且平面ABCD,ABEF互相垂直.点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
如图正方形ABCD,ABEF的边长都是1,而且平面ABCD,ABEF互相垂直.点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a< 已知:如图正方形ABCD的边长为a,P,Q分别为AB,DA上的点,当△PAQ的周长为2a时,求∠PCQ.
已知:如图正方形ABCD的边长为a,P,Q分别为AB,DA上的点,当△PAQ的周长为2a时,求∠PCQ. 如图正方形ABCD和四边形ADEF所在的平面垂直,FA⊥AD,DE∥FA,且
如图正方形ABCD和四边形ADEF所在的平面垂直,FA⊥AD,DE∥FA,且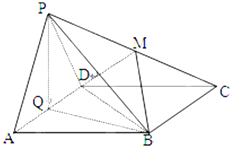 如图正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.