题目内容
(2012•青岛一模)已知函数f(x)=
x3-x.
(1)若不等式f(x)<k-2005对于x∈[-2,3]恒成立,求最小的正整数k;
(2)令函数g(x)=f(x)-
ax2+x(a≥2),求曲线y=g(x)在(1,g(1))处的切线与两坐标轴围成的三角形面积的最小值.
| 1 |
| 3 |
(1)若不等式f(x)<k-2005对于x∈[-2,3]恒成立,求最小的正整数k;
(2)令函数g(x)=f(x)-
| 1 |
| 2 |
分析:(1)由函数f(x)=
x3-x,知f′(x)=x2-1,令f′(x)=0,得x=±1,由此得到f(x)在x∈[-2,-1]上的最大值为f(3)=6,故要使得不等式f(x)<k-2005对于x∈[-2,3]恒成立,等价于6<k-2005恒成立,由此能求出最小的正整数k.
(2)由g(x)=f(x)-
ax2+x=
-
,知g′(x)=x2-ax,g(1)=
-
,故切线方程为y-(
-
)=(1-a)(x-1),与坐标轴的交点为(0,
-
),(
,0),由此能求出三角形面积的最小值.
| 1 |
| 3 |
(2)由g(x)=f(x)-
| 1 |
| 2 |
| x3 |
| 3 |
| ax2 |
| 2 |
| 1 |
| 3 |
| a |
| 2 |
| 1 |
| 3 |
| a |
| 2 |
| 2 |
| 3 |
| a |
| 2 |
| ||||
| 1-a |
解答:解:(1)∵函数f(x)=
x3-x,
∴f′(x)=x2-1,
令f′(x)=0,得x=±1,
当x∈[-2,-1]时,f′(x)>0,f(x)递增,
∴f(-2)=
×(-2)3-(-2)=-
,f(-1)=-
+1=
.
当x∈[-1,1]时,f′(x)<0,f(x)递减,f(1)=
-1=-
,
当x∈[1,3]时,f′(x)>0,f(x)递增,f(3)=
-3=6.
∴f(x)在x∈[-2,-1]上的最大值为f(3)=6,
要使得不等式f(x)<k-2005对于x∈[-2,3]恒成立,
则6<k-2005恒成立,解得k>2011,
所以最小的正整数k为2012.
(2)∵g(x)=f(x)-
ax2+x=
-
,
∴g′(x)=x2-ax,g(1)=
-
,
y=g(x)在(1,g(1))处的切线的斜率为g′(1)=1-a,
故切线方程为y-(
-
)=(1-a)(x-1),
化简得y-(1-a)x+
-a=0,与坐标轴的交点为(0,
-
),(
,0),
又∵a≥2,∴
-
<0,
>0,
所以面积S=
×(
-
)×
=
(
-
)2,
∵S为递增函数,
∴当a=2时,面积Smin=
×(1-
)2=
.
| 1 |
| 3 |
∴f′(x)=x2-1,
令f′(x)=0,得x=±1,
当x∈[-2,-1]时,f′(x)>0,f(x)递增,
∴f(-2)=
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
当x∈[-1,1]时,f′(x)<0,f(x)递减,f(1)=
| 1 |
| 3 |
| 2 |
| 3 |
当x∈[1,3]时,f′(x)>0,f(x)递增,f(3)=
| 27 |
| 3 |
∴f(x)在x∈[-2,-1]上的最大值为f(3)=6,
要使得不等式f(x)<k-2005对于x∈[-2,3]恒成立,
则6<k-2005恒成立,解得k>2011,
所以最小的正整数k为2012.
(2)∵g(x)=f(x)-
| 1 |
| 2 |
| x3 |
| 3 |
| ax2 |
| 2 |
∴g′(x)=x2-ax,g(1)=
| 1 |
| 3 |
| a |
| 2 |
y=g(x)在(1,g(1))处的切线的斜率为g′(1)=1-a,
故切线方程为y-(
| 1 |
| 3 |
| a |
| 2 |
化简得y-(1-a)x+
| 2 |
| 3 |
| 2 |
| 3 |
| a |
| 2 |
| ||||
| 1-a |
又∵a≥2,∴
| 2 |
| 3 |
| a |
| 2 |
| ||||
| 1-a |
所以面积S=
| 1 |
| 2 |
| a |
| 2 |
| 2 |
| 3 |
| ||||
| 1-a |
| 1 |
| 2(a-1) |
| a |
| 2 |
| 2 |
| 3 |
∵S为递增函数,
∴当a=2时,面积Smin=
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 18 |
点评:本题考查满足条件的最小实数值的求法,考查三角形面积的最小值的求法.综合性强,难度大,解题时要认真审题,注意导数性质、分类讨论思想、等价转化思想的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
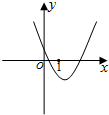 (2012•青岛一模)已知a>b,函数f(x)=(x-a)(x-b)的图象如图所示,则函数g(x)=loga(x+b)的图象可能为
(2012•青岛一模)已知a>b,函数f(x)=(x-a)(x-b)的图象如图所示,则函数g(x)=loga(x+b)的图象可能为