题目内容
设函数f（x）=x3+ax2-9x-1（a＜0），若曲线f（x）的斜率最小的切线与直线12x+y=6平行，则a的值为
- A.-3
- B.-12
- C.-1
- D.-9
A
分析：函数f′（x）=3x2+2ax-9，故当 x=-
时，f′（x）有最小值为3×
-
-9=-12，由此解得a的值．
解答：由题意可得 函数f′（x）=3x2+2ax-9，故当 x=- 时，其最小值等于3×-
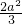-9=-12，
解得a=-3．
故选 A．
点评：本题考查函数的导数与切线的斜率的关系，二次函数的最小值的求法，求出函数f′（x）=3x2+2ax-9，是解题的突破口．
分析：函数f′（x）=3x2+2ax-9，故当 x=-
时，f′（x）有最小值为3×--9=-12，由此解得a的值．解答：由题意可得 函数f′（x）=3x2+2ax-9，故当 x=-
时，其最小值等于3×--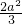9=-12，解得a=-3．
故选 A．
点评：本题考查函数的导数与切线的斜率的关系，二次函数的最小值的求法，求出函数f′（x）=3x2+2ax-9，是解题的突破口．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目