题目内容
抛物线y=2x2和x=2y2的焦点之间的距离为
- A.

- B.
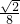
- C.

- D.

B
分析:分别把抛物线的方程整理成标准方程,然后求得各自的焦点坐标,进而利用两点间的距离公式求得答案.
解答:整理抛物线y=2x2,得x2= y,焦点为(0,
y,焦点为(0, )
)
整理抛物线x=2y2,得y2= x,焦点为(
x,焦点为( ,0),
,0),
∴焦点之间的距离为 =
=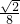
故选B
点评:本题主要考查了抛物线的简单性质.解题的时候要注意焦点所在的坐标轴的位置.
分析:分别把抛物线的方程整理成标准方程,然后求得各自的焦点坐标,进而利用两点间的距离公式求得答案.
解答:整理抛物线y=2x2,得x2=
 y,焦点为(0,
y,焦点为(0, )
)整理抛物线x=2y2,得y2=
 x,焦点为(
x,焦点为( ,0),
,0),∴焦点之间的距离为
 =
=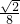
故选B
点评:本题主要考查了抛物线的简单性质.解题的时候要注意焦点所在的坐标轴的位置.

练习册系列答案
相关题目
抛物线y=2x2和x=2y2的焦点之间的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
对于函数y=2x2-2x+a (其中a是可变常数)的性质下列叙述正确的是( )
|
(A) 其图像是和抛物线y=2x2形状相同,顶点在直线 |
|
(B) 其图像是和抛物线y=x2形状相同,顶点在直线 |
|
(C) 其图像是和抛物线y=2x2形状相同,顶点在直线x=1上滑动的抛物线系 |
|
(D) 其图像是和抛物线y=2x2形状相同,顶点在直线 |



