题目内容
(1)若角α是第二象限角,化简tanα
|
(2)化简:
| ||
sin130°+
|
分析:(1)根据象限三角函数的符号,直接化简表达式,求出最简结果.
(2)利用平方关系,以及三角函数在象限的符号,去掉根号和绝对值符号,化简即可.
(2)利用平方关系,以及三角函数在象限的符号,去掉根号和绝对值符号,化简即可.
解答:解:(1)原式=tanα
=tanα
=
|
|,
∵α是第二象限角,∴sinα>0,cosα<0,
∴原式=
;
|
|=
•
=-1.
(2)原式=
=
=
=1.
|
|
| sinα |
| cosα |
| cosα |
| sinα |
∵α是第二象限角,∴sinα>0,cosα<0,
∴原式=
|
| sinα |
| cosα |
| cosα |
| sinα |
| sinα |
| cosα |
| -cosα |
| sinα |
(2)原式=
| ||
sin130°+
|
=
| |sin130°-cos130°| |
| sin130°+|cos130°| |
| sin130°-cos130° |
| sin130°-cos130° |
点评:本题考查同角三角函数基本关系式的应用,考查计算能力,推理能力,是基础题.

练习册系列答案
相关题目
 >cos
>cos ,则
,则  .
.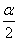 所在的象限;
所在的象限;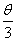 的终边相同的角.
的终边相同的角.  >cos
>cos ,且sin
,且sin >cos
>cos ;
; ,则
,则  .
.