题目内容
下列命题中正确的是
①空间中三个平面α,β,γ,若α⊥β,γ⊥β,则α∥γ
②空间中两个平面α,β,若α∥β,直线a与α所成角等于直线b与β所成角,则a∥b.
③球O与棱长为a正四面体各面都相切,则该球的表面积为
a2;
④三棱锥P-ABC中,PA⊥BC,PB⊥AC,则PC⊥AB.
③④
③④
(填上你认为所有正确的选项)①空间中三个平面α,β,γ,若α⊥β,γ⊥β,则α∥γ
②空间中两个平面α,β,若α∥β,直线a与α所成角等于直线b与β所成角,则a∥b.
③球O与棱长为a正四面体各面都相切,则该球的表面积为
| π | 6 |
④三棱锥P-ABC中,PA⊥BC,PB⊥AC,则PC⊥AB.
分析:①根据面面垂直的几何特征可以判断真假,也可举反例说明;
②a与b平行或异面,平行是两个角的方向相同,异面是两个角的方向不同,从而可判定②的真假
③作出正四面体的图形,球的球心位置,说明OE是内切球的半径,利用直角三角形,逐步求出内切球的表面积,从而可判定③的真假;
④设P在面ABC的射影为P′,然后利用三垂线定理可证明.
②a与b平行或异面,平行是两个角的方向相同,异面是两个角的方向不同,从而可判定②的真假
③作出正四面体的图形,球的球心位置,说明OE是内切球的半径,利用直角三角形,逐步求出内切球的表面积,从而可判定③的真假;
④设P在面ABC的射影为P′,然后利用三垂线定理可证明.
解答:解:①若α⊥γ,β⊥γ,则平面α与平面β可能平行也可能相交,如一本书打开立在桌面上此时两平面相交,故①错误;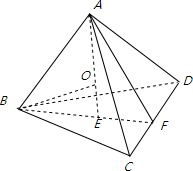
②空间中两个平面α,β,若α∥β,直线a与α所成角等于直线b与β所成角,则a与b平行或异面,平行是两个角的方向相同,异面是两个角的方向不同,故②不正确;
③如图O为正四面体ABCD的内切球的球心,正四面体的棱长为:a;
所以OE为内切球的半径,BF=AF=
BE=
,所以AE=
=
,
BO2-OE2=BE2,(
-OE)2-OE2=(
)2
所以 OE=
球的表面积为:4π•OE2=
a2故③正确;
④设P在面ABC的射影为P′
∵PA⊥BC,PB⊥AC
∴P′A⊥BC,P′B⊥AC
连接P′C
∵三角形的三个高相交于一点
∴P′C⊥AB
∴PC⊥AB故④正确.
故答案为:③④.

②空间中两个平面α,β,若α∥β,直线a与α所成角等于直线b与β所成角,则a与b平行或异面,平行是两个角的方向相同,异面是两个角的方向不同,故②不正确;
③如图O为正四面体ABCD的内切球的球心,正四面体的棱长为:a;
所以OE为内切球的半径,BF=AF=
| ||
| 2 |
BE=
| ||
| 3 |
a2-(
|
| ||
| 3 |
BO2-OE2=BE2,(
| ||
| 3 |
| ||
| 3 |
所以 OE=
| ||
| 12 |
球的表面积为:4π•OE2=
| π |
| 6 |
④设P在面ABC的射影为P′
∵PA⊥BC,PB⊥AC
∴P′A⊥BC,P′B⊥AC
连接P′C
∵三角形的三个高相交于一点
∴P′C⊥AB
∴PC⊥AB故④正确.
故答案为:③④.
点评:本题考查空间中直线与平面之间的位置关系,正四面体的内切球的表面积,是一道典型题目,考试常考题,考查空间想象能力,计算能力,是基础题.

练习册系列答案
相关题目