题目内容
已知在△ABC中，AB=AC=2，BC=2
，点P为边BC所在直线上的一个动点，则关于
?(
+
)的值，正确的是（ ）
| 3 |
| AP |
| AB |
| AC |
| A、为定值2 |
| B、最大值为4 |
| C、最小值为1 |
| D、与P的位置有关 |
分析：取BC的中点D，连结AD，可得AD⊥BC，利用勾股定理算出AD=1．根据根据向量加法的平行四边形法则得
+
=2
，结合
=
+
可得
•(
+
)=2
•（
+
）=2
2+
•
，再根据
•
=0，代入计算可得
•(
+
)为定值2．
| AB |
| AC |
| AD |
| AP |
| AD |
| DP |
| AP |
| AB |
| AC |
| AD |
| AD |
| DP |
| AD |
| AD |
| DP |
| AD |
| DP |
| AP |
| AB |
| AC |
解答：解：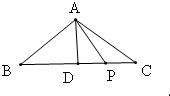
取BC的中点D，连结AD．
∵在△ABC中，AB=AC=2，BC=2
，
∴AD⊥BC，AD=
=1．
∵D为BC中点，
∴根据向量加法的平行四边形法则，可得
+
=2
，
又∵
=
+
，
∴
•(
+
)=2
•（
+
）=2
2+
•
，
∵
⊥
，可得
•
=0，
∴
•(
+
)=2
2=2|
|2=2×12=2．即
•(
+
)为定值2．
故选：A
取BC的中点D，连结AD．∵在△ABC中，AB=AC=2，BC=2
| 3 |
∴AD⊥BC，AD=
| AB2-BD2 |
∵D为BC中点，
∴根据向量加法的平行四边形法则，可得
| AB |
| AC |
| AD |
又∵
| AP |
| AD |
| DP |
∴
| AP |
| AB |
| AC |
| AD |
| AD |
| DP |
| AD |
| AD |
| DP |
∵
| AD |
| DP |
| AD |
| DP |
∴
| AP |
| AB |
| AC |
| AD |
| AD |
| AP |
| AB |
| AC |
故选：A
点评：本题在等腰三角形中探索向量的数量积是否为定值．着重考查了向量加法法则、向量的数量积及其运算性质、等腰三角形的性质与勾股定理等知识，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目