题目内容
(本小题满分13分)已知:函数 对一切实数
对一切实数 都有
都有

 成立,且
成立,且 .
.
(1)求 的值;
的值;
(2)求 的解析式;
的解析式;
(3)已知 ,设P:当
,设P:当 时,不等式
时,不等式 恒成立;Q:当
恒成立;Q:当 时,
时, 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的 的集合记为
的集合记为 ,满足Q成立的
,满足Q成立的 的集合记为
的集合记为 ,求
,求 ∩
∩ (
( 为全集)
为全集)
 对一切实数
对一切实数 都有
都有
 成立,且
成立,且 .
.(1)求
 的值;
的值;(2)求
 的解析式;
的解析式; (3)已知
 ,设P:当
,设P:当 时,不等式
时,不等式 恒成立;Q:当
恒成立;Q:当 时,
时, 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的 的集合记为
的集合记为 ,满足Q成立的
,满足Q成立的 的集合记为
的集合记为 ,求
,求 ∩
∩ (
( 为全集)
为全集)(1)-2
(2)

(3)

解:(1)令 ,则由已知
,则由已知
∴
(2)令 , 则
, 则
又∵ ∴
∴
(3)不等式 即
即
即 当
当 时,
时, , 又
, 又 恒成立 故
恒成立 故

又 在
在 上是单调函数,故有
上是单调函数,故有
∴
∴ ∩
∩ =
=
 ,则由已知
,则由已知
∴

(2)令
 , 则
, 则
又∵
 ∴
∴
(3)不等式
 即
即
即
 当
当 时,
时, , 又
, 又 恒成立 故
恒成立 故

又
 在
在 上是单调函数,故有
上是单调函数,故有
∴

∴
 ∩
∩ =
=

练习册系列答案
相关题目
 ,
, 则
则 之间的大小关系为
之间的大小关系为 <
< <
<
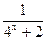 (x∈R),P1(x1,y1),P2(x2,y2)是函数y=f(x)图像上两点,且线段P1P2中点P的横坐标为
(x∈R),P1(x1,y1),P2(x2,y2)是函数y=f(x)图像上两点,且线段P1P2中点P的横坐标为 。
。 }的通项公式为
}的通项公式为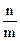 )(m∈N
)(m∈N ,n=1,2,3,…,m),求数列{
,n=1,2,3,…,m),求数列{ ; (5分)
; (5分)
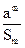 <
< 横成立,求实数a的取值范围。(3分)
横成立,求实数a的取值范围。(3分) 有实数根
有实数根 ,则复数
,则复数 __________________.
__________________. 的对应法则
的对应法则 :
: (
( ,则A中的元素3在B中与之对应的元素是 ★
,则A中的元素3在B中与之对应的元素是 ★  0,1)
0,1)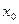 是方程
是方程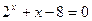 的解,且
的解,且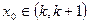 ,
,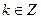 ,则
,则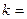 ___________.
___________. ,且
,且 ,则与A中的元素
,则与A中的元素 对应的B中的元素为( )
对应的B中的元素为( )


