题目内容
（文科）设函数f（x）的定义域为{x|x＞0}，值域为R，且同时满足下列条件：
（1）对于任意正数x1，x2，都有f（x1x2）=f（x1）+f（x2）；
（2）对于任意正数x1，x2，且x1≠x2，都有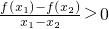
写出符合上述条件的一个函数f（x）________．
解：对于性质（1），函数y=logax满足对于任意正数x1，x2，都有loga（x1x2）=logax1+logax2，
再看性质（2），说明函数是定义在（0，+∞）的增函数．
由以上可得，取底数a=2，可得函数y=log2x就是满足条件的一个函数．
故答案为：y=log2x
分析：根据性质（1）联想到对数函数y=logax满足条件，再根据性质（2）得到函数是定义在（0，+∞）的增函数．由此，不难找到符合题意的函数f（x）．
点评：本题以抽象函数为例，叫我们找出符合题意的一个具体函数，着重考查了函数的简单性质和基本初等函数等知识，属于基础题．
再看性质（2），说明函数是定义在（0，+∞）的增函数．
由以上可得，取底数a=2，可得函数y=log2x就是满足条件的一个函数．
故答案为：y=log2x
分析：根据性质（1）联想到对数函数y=logax满足条件，再根据性质（2）得到函数是定义在（0，+∞）的增函数．由此，不难找到符合题意的函数f（x）．
点评：本题以抽象函数为例，叫我们找出符合题意的一个具体函数，着重考查了函数的简单性质和基本初等函数等知识，属于基础题．
练习册系列答案
相关题目
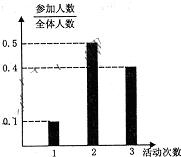（理科）某中学号召学生在2010年春节期间至少参加一次社会公益活动（下面简称为“活动”）．该校合唱团共有100名学生，他们参加活动的次数统计如图所示．