题目内容

设定义域为R的函数f（x）=
|lg|x-2||(x≠2)
0
，若b＜0，则关于x的方程f2（x）+bf（x）=0的不同实根共有（　　）
A．4个B．5个C．7个D．8个
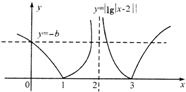
精英家教网
y=|lg|x-2||的大致图象如图所示，
而方程f2（x）+bf（x）=0，即f（x）[f（x）+b]=0，
则化成f（x）=0或f（x）=-b＞0（b＜0）两个方程
如图，f（x）=0有2个根，f（x）=-b有4个根，
再加上x=2时，f（x）=0一个根，综合共有7个根，
故选C
练习册系列答案
相关题目
设定义域为R的函数f(x)=
5|x-1|-1，x≥0
x2+4x+4，x＜0
若关于x的方程f2（x）-（2m+1）f（x）+m2=0有7个不同的实数根，则实数m=
 
．
设定义域为R的函数f(x)=
5|x-1|-1，x≥0
x2+4x+4，x＜0
若关于x的方程f2（x）-（2m+1）f（x）+m2=0有5个不同的实数解，则m=（　　）
设定义域为R的函数f(x)=
-2x+a2x+1+b
（a，b为实数）若f（x）是奇函数．
（1）求a与b的值；
（2）判断函数f（x）的单调性，并证明；
（3）证明对任何实数x、c都有f（x）＜c2-3c+3成立．
设定义域为R的函数f（x）=
|lg|x-1||，x≠1
0，          x=1
，则关于x的方程f2（x）+bf（x）+c=0有7个不同实数解的充要条件是 （　　）
设定义域为R的函数f(x)=
4
|x-1
(x≠1)
2
 (x=1)
，若关于x的方程f2（x）+bf（x）+c=0有三个不同的实数解x1、x2、x3，则x12+x22|x32等于（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网