题目内容
已知
，
，那么
的值为
- A.
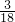
- B.
- C.
- D.
C
分析：把所求的式子中的角α+
变为（α+β）-（β-），然后利用两角差的正切函数公式化简后，把已知的tan（α+β）和tan（β-）的值代入即可求出值．
解答：由，，
则tan（α+）=tan[（α+β）-（β-）]=
=
=．
故选C
点评：此题考查学生灵活运用两角差的正切函数公式化简求值，是一道基础题．学生做题时应注意角度的灵活变换．
分析：把所求的式子中的角α+
变为（α+β）-（β-），然后利用两角差的正切函数公式化简后，把已知的tan（α+β）和tan（β-）的值代入即可求出值．解答：由
，，则tan（α+
）=tan[（α+β）-（β-）]===．故选C
点评：此题考查学生灵活运用两角差的正切函数公式化简求值，是一道基础题．学生做题时应注意角度的灵活变换．
练习册系列答案
相关题目
，那么
的值为 ( )
C．
D．
，那么
的值为
C．
D．
，那么
的值为
B. 
C. 
D. 
，那么
的值为( ※ )已知函数
，那么
的值为 ( )
| A． 9 | B． | C． | D． |