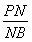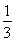题目内容
在直角坐标系xOy中，椭圆C的参数方程为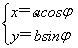
(φ为参数，a>b>0)．在极坐标系(与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴)中，直线l与圆O的极坐标方程分别为ρsin 
＝
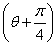m(m为非零常数)与ρ＝b.若直线l经过椭圆C的焦点，且与圆O相切，则椭圆C的离心率为________．
【解析】由已知可得椭圆标准方程为
＝1(a>b>0)．
由ρsin 
＝
m可得ρsin θ＋ρcos θ＝m，即直线的普通方程为x＋y＝m.又圆的普通方程为x2＋y2＝b2，不妨设直线l经过椭圆C的右焦点(c,0)，则得c＝m.又因为直线l与圆O相切，所以
＝b，因此c＝
b，即c2＝2(a2－c2)．整理，得
＝
，故椭圆C的离心率为e＝.
练习册系列答案
相关题目
