题目内容
已知函数 .
.
(1)求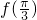 的值;
的值;
(2)求f(x)的单调递减区间.
解:(1) .
.
(2) =
=
= =
= .
.
由 (k∈Z).
(k∈Z).
得 ,
,
∴f(x)的递减区间为 (k∈Z).
(k∈Z).
分析:(1)直接把x= 代入函数表达式,求出函数值即可.
代入函数表达式,求出函数值即可.
(2)利用诱导公式和两角和的正弦函数化简函数 为
为 ,根据正弦函数的单调减区间,
,根据正弦函数的单调减区间,
求出f(x)的单调递减区间.
点评:本题是基础题,考查函数值的求法,正弦函数的化简,单调减区间的求法,能够正确利用诱导公式以及和角公式化简,是本题的前提,基本函数的基本性质是解题的关键.
 .
.(2)
 =
=
=
 =
= .
.由
 (k∈Z).
(k∈Z).得
 ,
,∴f(x)的递减区间为
 (k∈Z).
(k∈Z).分析:(1)直接把x=
 代入函数表达式,求出函数值即可.
代入函数表达式,求出函数值即可.(2)利用诱导公式和两角和的正弦函数化简函数
 为
为 ,根据正弦函数的单调减区间,
,根据正弦函数的单调减区间,求出f(x)的单调递减区间.
点评:本题是基础题,考查函数值的求法,正弦函数的化简,单调减区间的求法,能够正确利用诱导公式以及和角公式化简,是本题的前提,基本函数的基本性质是解题的关键.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 .
. 的值;
的值;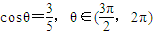 ,求
,求 .
. .
. 的值;
的值; .
. 的单调区间;
的单调区间; ,若对任意
,若对任意 ,总存在
,总存在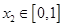 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.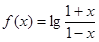 ,(1)求
,(1)求 的定义域;
(2)使
的定义域;
(2)使 的
的 的取值范围.
的取值范围. ,(1)求
,(1)求 的最小正周期;(2)求
的最小正周期;(2)求 的集合。
的集合。