题目内容
已知数列{an}的前n项和为Sn,且a1=1,a2=3,2Sn﹣(n+1)an=An+B(其中A、B是常数,n∈N*).
(1)求A、B的值;
(2)求证数列 是等差数列,并求数列{an}的通项公式an;
是等差数列,并求数列{an}的通项公式an;
(3)已知k是正整数,不等式8a n+1﹣an2<k对n∈N*都成立,求k的最小值.
(1)求A、B的值;
(2)求证数列
 是等差数列,并求数列{an}的通项公式an;
是等差数列,并求数列{an}的通项公式an;(3)已知k是正整数,不等式8a n+1﹣an2<k对n∈N*都成立,求k的最小值.
解:(1)∵a1=1,a2=3,2Sn﹣(n+1)an=An+B(n∈N*),
分别取n=1和n=2,
得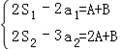 ,
,
即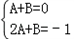 ,
,
解得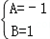 .
.
(2)由(1)知,2Sn﹣(n+1)an=﹣n+1(n∈N*),
∴2Sn+1﹣(n+2)an+1=﹣n,
得2a n+1﹣(n+2)a n+1+(n+1)an=﹣1,即na n+1﹣(n+1)an=1.
两边同除以n(n+1),
可化为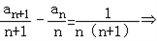
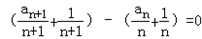 .
.
数列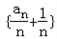 是以
是以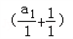 为首项,公差为零的等差数列,
为首项,公差为零的等差数列,
于是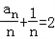 .
.
∴数列{an}的通项公式为an=2n﹣1(n∈N*).
(3)由(2)知,an=2n﹣1(n∈N*).
又8a n+1﹣an2<k,即8(2n+1)﹣(2n﹣1)2<k,
进一步可化为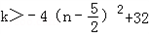 .
.
当n=2或3时,﹣4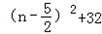 的最大值为31,
的最大值为31,
因此,只要k>31即满足要求,
又k是正整数,k的最小值为32.
分别取n=1和n=2,
得
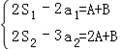 ,
,即
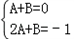 ,
,解得
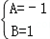 .
.(2)由(1)知,2Sn﹣(n+1)an=﹣n+1(n∈N*),
∴2Sn+1﹣(n+2)an+1=﹣n,
得2a n+1﹣(n+2)a n+1+(n+1)an=﹣1,即na n+1﹣(n+1)an=1.
两边同除以n(n+1),
可化为
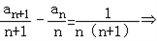
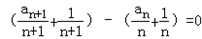 .
.数列
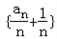 是以
是以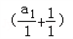 为首项,公差为零的等差数列,
为首项,公差为零的等差数列,于是
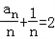 .
.∴数列{an}的通项公式为an=2n﹣1(n∈N*).
(3)由(2)知,an=2n﹣1(n∈N*).
又8a n+1﹣an2<k,即8(2n+1)﹣(2n﹣1)2<k,
进一步可化为
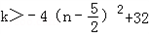 .
.当n=2或3时,﹣4
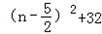 的最大值为31,
的最大值为31,因此,只要k>31即满足要求,
又k是正整数,k的最小值为32.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |