题目内容
设F1，F2是双曲线
的左、右两个焦点，若双曲线右支上存在一点P，使
（O为原点坐标）且|PF1|=λ|PF2|，则λ的值为 ．
【答案】分析：由已知中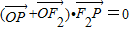
可得
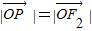，根据直角三角形斜边上的中线等于斜边的一半，可得△PF1F2是以P为直角的直角三角形，进而根据P是双曲线右支上的点，及双曲线的性质结合勾股定理构造方程可得|PF2|，|PF1|，进而求出λ的值．
解答：解：由双曲线方程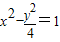
可得
a=1，b=2，c=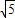
，
∴
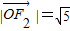
又∵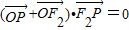
∴
∴
∴
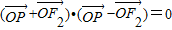
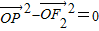
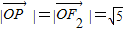
故△PF1F2是以P为直角的直角三角形
又∵P是双曲线右支上的点
∴|PF1|＞|PF2|，
∴|PF1|=|PF2|+2，
由勾股定理可得|PF1|2+（|PF2|+2）2=4C2=20
解得|PF2|=2，|PF1|=4
故λ=2
故答案为2
点评：本题考查的知识点是双曲线的简单性质，平面向量的数量积运算，其中根据已知中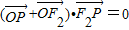
可得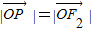
，进而判断出△PF1F2是以P为直角的直角三角形是解答的关键．
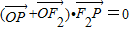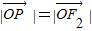可得，根据直角三角形斜边上的中线等于斜边的一半，可得△PF1F2是以P为直角的直角三角形，进而根据P是双曲线右支上的点，及双曲线的性质结合勾股定理构造方程可得|PF2|，|PF1|，进而求出λ的值．解答：解：由双曲线方程
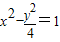可得a=1，b=2，c=
，∴
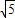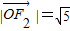
又∵
∴
∴
∴
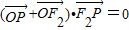
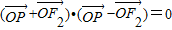
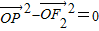
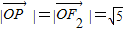
故△PF1F2是以P为直角的直角三角形
又∵P是双曲线右支上的点
∴|PF1|＞|PF2|，
∴|PF1|=|PF2|+2，
由勾股定理可得|PF1|2+（|PF2|+2）2=4C2=20
解得|PF2|=2，|PF1|=4
故λ=2
故答案为2
点评：本题考查的知识点是双曲线的简单性质，平面向量的数量积运算，其中根据已知中
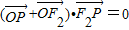可得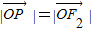，进而判断出△PF1F2是以P为直角的直角三角形是解答的关键． 
练习册系列答案
相关题目