题目内容
判断下列函数的奇偶性:
(1)f(x)=x4+x;
(2)f(x)=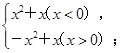
(3)f(x)=lg(x+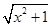 ).
).
(1)既不是奇函数也不是偶函数(2)奇函数(3)奇函数
解析

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
题目内容
判断下列函数的奇偶性:
(1)f(x)=x4+x;
(2)f(x)=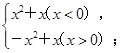
(3)f(x)=lg(x+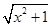 ).
).
(1)既不是奇函数也不是偶函数(2)奇函数(3)奇函数
解析

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案