题目内容
若 ,且
,且 ,则α+β等于
,则α+β等于
- A.

- B.

- C.

- D.

B
分析:根据角的范围以及同角三角函数的基本关系,求出sin(α-β) 和sin2α 的值,由 cos(α+β)=cos[2α-(α-β)],
利用两角差的余弦公式求出cos(α+β)值.
解答:由题意可得 0<α-β<π,2α∈(0,π),又 ,
,
∴sin(α-β)=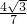 ,sin2α=
,sin2α=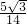 .
.
∴cos(α+β)=cos[2α-(α-β)]=cos2α cos(α-β)+sin2α sin(α-β)= +
+
= =
= .
.
再由 可得 α+β=
可得 α+β= ,
,
故选:B.
点评:本题主要考查两角差的余弦公式,同角三角函数的基本关系,注意角之间的关系及角的范围.
分析:根据角的范围以及同角三角函数的基本关系,求出sin(α-β) 和sin2α 的值,由 cos(α+β)=cos[2α-(α-β)],
利用两角差的余弦公式求出cos(α+β)值.
解答:由题意可得 0<α-β<π,2α∈(0,π),又
 ,
,∴sin(α-β)=
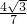 ,sin2α=
,sin2α=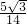 .
.∴cos(α+β)=cos[2α-(α-β)]=cos2α cos(α-β)+sin2α sin(α-β)=
 +
+
=
 =
= .
.再由
 可得 α+β=
可得 α+β= ,
,故选:B.
点评:本题主要考查两角差的余弦公式,同角三角函数的基本关系,注意角之间的关系及角的范围.

练习册系列答案
相关题目
 外接圆的半径为1,圆心为O.若
外接圆的半径为1,圆心为O.若 ,且
,且 ,则
,则 等于( )
等于( ) (B)
(B)  (C)
(C)
 (D)3
(D)3 =
= ,且
,且 ,则
,则 等于
等于
 B.
B.  C.
C. D.
D.
 ,且
,且 ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.
 =
= ,且
,且 ,则
,则 等于 ( )
A.—502.5
B.—1004
C.502.5
D.1004
等于 ( )
A.—502.5
B.—1004
C.502.5
D.1004